Содержание
| Ведение …………………………………………………………………………………… | |
| Раздел 1 Плоскость ……………………………………………………………………. | |
| 1.1 Уравнение поверхности ……………………………………………………………… | |
| 1.2 Условия определяющие плоскость в пространстве ………………………………... | |
| 1.3 Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору ……………………………………………………………………………… | |
| 1.4 Общее уравнение плоскости ………………………………………………………... | |
| 1.5 Исследование общего уравнения плоскости ……………………………………….. | |
| 1.6 Уравнение плоскости в отрезках ……………………………………………………. | |
| 1.7 Уравнение плоскости, проходящей через три точки | |
| 1.8 Взаимное расположение плоскостей в пространстве. Угол между плоскостями | |
| 1.9 Расстояние от точки до плоскости …………………………………………………... | |
| 1.10 Решение задач на составление уравнений плоскости …………………………….. | |
| Раздел 2 Уравнения прямой в пространстве ………………………………………… | |
| 2.1 Уравнение линии в пространстве …………………………………………………… | |
| 2.2 Общее уравнение прямой …………………………………………………………… | |
| 2.3 Условия, определяющие прямую в пространстве ………………………………… | |
| 2.4 Уравнение прямой, проходящей через данному точку параллельно данному вектору ………………………………………………………………………………………... | |
| 2.5 Параметрические уравнения прямой ………………………………………………... | |
| 2.6 Уравнение прямой, проходящей через две точки ………………………………….. | |
| 2.7 Решение задач на составление уравнений прямой в пространстве ……………….. | |
| 2.8 Переход от общего уравнения прямой к каноническим уравнениям …………….. | |
| 2.9 Вычисление координат точки пересечения прямой с плоскостью ……………….. | |
| 2.10 Проекция точки на плоскость ……………………………………………………… | |
| 2.11 Проекция точки на прямую ………………………………………………………… | |
| 2.12 Взаимное расположение прямых ………………………………………………….. | |
| Раздел 3 Дополнительные уравнения плоскости …………………………………… | |
| 3.1 Уравнение плоскости проходящей через две пересекающиеся прямые ………….. | |
| 3.2 Уравнение плоскости проходящей через две параллельные прямые …………….. | |
| 3.3 Уравнение плоскости проходящей через прямую и точку, не принадлежащую данной прямой ……………………………………………………………………………. | |
| 3.4 Взаимное расположение прямой и плоскости в пространстве ……………………. | |
| 3.5 Угол между прямыми, прямой и плоскостью в пространстве ……………………. | |
| 3.6 Задачи для самостоятельного решения ……………………………………………. | |
| Приложение А Базовые уравнения, формулы и понятия ………………………… |
Введение
Данное учебное пособие «Прямая и плоскость в пространстве» ориентировано на подготовку студентов специальности 230115 Программирование в компьютерных системах.
Специалист данной отрасли должен владеть аналитическим мышлением, рациональными приёмами моделирования математического программного обеспечения, уметь использовать математические знания в будущей практической работе.
Данное учебное пособие состоит из трех разделов, каждый из которых содержит значительный объём теоретического материала по базовым знаниям модуля ЕН.01.М.06 «Аналитическая геометрия в пространстве».
Вместе с тем оно имеет практическую направленность, в него включены типовые задачи и даются методы их решения. Это помогает студентам ориентироваться в решении всех основных типов задач на основе логического исследования, выявления проблем и поисков их решения.
Рассматриваются задания разных уровней трудности и широкой вариативности. Этим обеспечивается уровневый характер учения студентов, их постепенная адаптация в освоении содержания учебных элементов УЭ.06.02 «Плоскость» и УЭ.06.03 «Прямая в пространстве»
По данным элементам в пособии даны выводы основных уравнений плоскости и прямой в пространстве, представлены образцы решения типовых задач и задачи для самостоятельного решения. Задачи для самостоятельного решения выделены жирным шрифтом. Тексты задач представлены в таблице 1.
Таблица 1
| № | Условия задачи | Ответ |
Составить уравнение плоскости α, проходящей через точку N(2,-2,0) перпендикулярно вектору 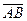 : А(5,0,1), В(3,2,-2) : А(5,0,1), В(3,2,-2) | 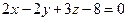 | |
| Составить уравнение плоскости, проходящей через три точки: А(1, -6, 7), В(4,5,-3) и С(3,0,2) | 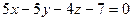 | |
Найти расстояние между параллельными плоскостями 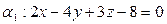 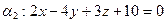 | 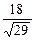 | |
Составить уравнение плоскости, проходящей через начало координат и точки: 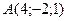 и и 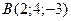 | 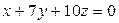 | |
Составить уравнение плоскости 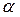 , проходящей через точки , проходящей через точки 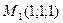 и и 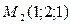 параллельно вектору параллельно вектору 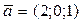 | 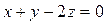 | |
Составить уравнение плоскости 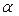 , проходящей через точку , проходящей через точку 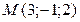 параллельно плоскости параллельно плоскости 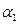 : : 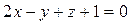 | 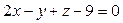 | |
Составить уравнение плоскости 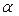 , проходящей через ось OZ и точку , проходящей через ось OZ и точку 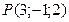 | 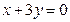 |
 2015-06-28
2015-06-28 768
768







