Пусть нужно найти значение предела функции 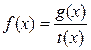 при
при 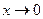 , и при этом
, и при этом
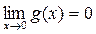 и
и 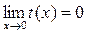 , то есть функции являются бесконечно малыми.
, то есть функции являются бесконечно малыми.
Функции 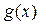 и
и 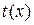 называются бесконечно малыми одного порядка, если
называются бесконечно малыми одного порядка, если
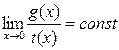 и
и
эквивалентными бесконечно малыми, если 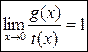
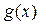
Важно, что эквивалентные бесконечно малые функции могут заменять друг друга при вычислении пределов функций.
Таблицу эквивалентных бесконечно малых функций можно составить по известным действиям с первым и вторым замечательными пределами:
Из первого замечательного предела 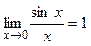 следует, что
следует, что
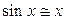
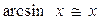
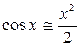
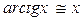
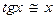
Из второго замечательного предела 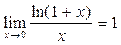
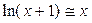
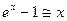
Пример 1. Вычислить предел 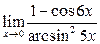 .
.
Из таблицы эквивалентных бесконечно малых очевидно, что 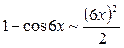 , то есть
, то есть 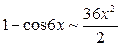 и
и 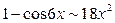 , и
, и 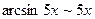 .
.
Следовательно,
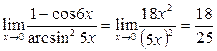
Пример 2. Вычислить предел 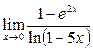 .
.
Из таблицы эквивалентных бесконечно малых следует, что
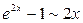 , и
, и 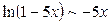 .
.
Следовательно, 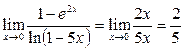
Пример 3. 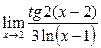
Для приведения выражения к бесконечно малым нужно выполнить замену переменной
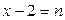 ,
,
тогда функция примет вид:
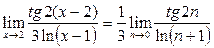
На основе замены функций на эквивалентные бесконечно малые можно записать:
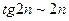 и
и 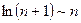 .
.
И тогда 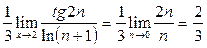
 2015-06-28
2015-06-28 1938
1938