Определение. Если 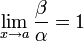, то бесконечно малые величины 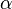и называются эквивалентными ( )

Если , то бесконечно малые величины и 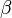называются эквивалентными ().

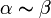Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При 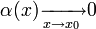справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

·

·

·

·

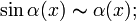
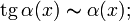
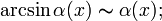
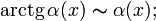
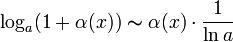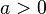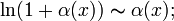
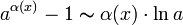· , где ;

·

· , где ;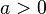

·

·

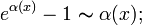
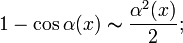
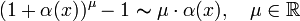· , поэтому используют выражение:

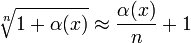, где .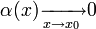

Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).