Определение1: Число 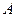 называется пределом функции
называется пределом функции 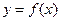 , если для любого числа
, если для любого числа 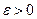 существует
существует 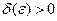 (дельта от эпсилон), что для всех
(дельта от эпсилон), что для всех 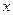 , удовлетворяющих условию
, удовлетворяющих условию 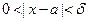 выполняется неравенство
выполняется неравенство 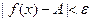 .
.
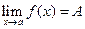 или
или 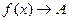 при
при 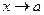 .
.
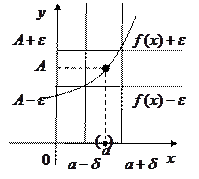 |
Иллюстрация:
Замечательные пределы:
Первый замечательный предел: 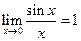 (при
(при 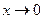 значение функции
значение функции 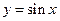 )
)
Второй замечательный предел: 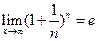 (иррациональное число
(иррациональное число 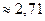 )
)
Способы нахождения пределов
1. Подстановка в данное выражение предельного значения аргумента:
а) 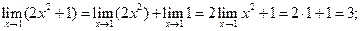
б) 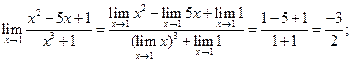
2. Предел числителя не равен нулю (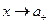 справа и
справа и 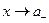 слева):
слева):
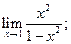 рассматриваем
рассматриваем 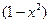
при 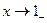 и
и 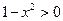 , то
, то 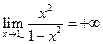
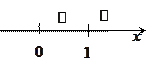 |
если
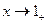 и
и 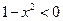 , то
, то 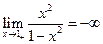
3. Предел числителя равен нулю:
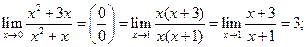 (упрощение выражений, стоящих под знаком предела)
(упрощение выражений, стоящих под знаком предела)
4. Вычисление предела при 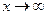 :
:
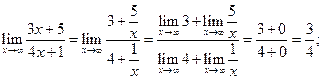 (почленное деление на
(почленное деление на 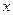 в наибольшей степени)
в наибольшей степени)
 2015-06-28
2015-06-28 363
363








