Функцией распределения (интегральной функцией) случайной величины 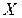 называется функция
называется функция 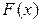 действительной переменной
действительной переменной 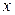 , определяемая равенством:
, определяемая равенством: 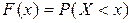 , где
, где 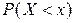 – вероятность того, что случайная величина
– вероятность того, что случайная величина 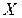 принимает значение меньшее
принимает значение меньшее 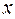 . Вероятность того, что случайная величина
. Вероятность того, что случайная величина 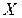 примет значение из полуинтервала
примет значение из полуинтервала 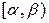 , равна разности значений ее функции распределения в концах этого промежутка
, равна разности значений ее функции распределения в концах этого промежутка 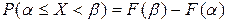 .
.
Свойства функции распределения:
1. Все значения функции распределения принадлежат отрезку 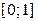 , т.е.
, т.е. 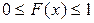 . Это следует из определения функции распределения и свойств вероятности.
. Это следует из определения функции распределения и свойств вероятности.
2. Функция распределения 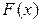 является неубывающей, т.е. если
является неубывающей, т.е. если 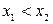 , то
, то 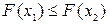 .
.
3. Функция 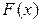 в точке
в точке 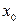 непрерывна слева, т.е.
непрерывна слева, т.е. 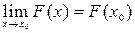 при любом
при любом 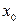 .
.
4. Вероятность того, что непрерывная случайная величина 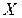 примет какое-либо заранее заданное значение, равна нулю:
примет какое-либо заранее заданное значение, равна нулю: 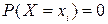 .
.
5. Если возможные значение случайной величины 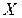 принадлежат интервалу
принадлежат интервалу 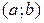 то:
то:
а) 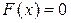 при
при 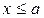 ;
;
б) 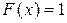 при
при 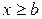 .
.
Следствие: если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения: 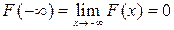 ;
; 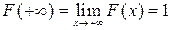 .
.
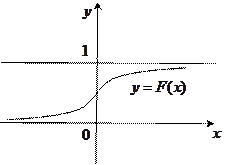 |
График функции распределения целиком расположен в полосе между прямыми
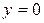 и
и 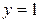 .
.
Плотностью распределения вероятностей непрерывной случайной величины 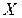 (дифференциальной функцией распределения) называется функция
(дифференциальной функцией распределения) называется функция 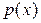 , равная производной интегральной функции распределения:
, равная производной интегральной функции распределения: 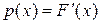 . График функции
. График функции 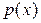 называется кривой распределения.
называется кривой распределения.
Вероятностью попадании непрерывной случайной величины 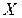 в интервал
в интервал 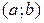 равна определенному интегралу от ее плотности вероятности, взятому в пределах от
равна определенному интегралу от ее плотности вероятности, взятому в пределах от 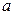 до
до 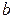 :
: 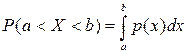 .
.
Распределение вероятностей непрерывной случайной величины 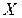 , принимающей все свои значения на отрезке
, принимающей все свои значения на отрезке 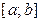 , называется равномерным, если ее плотность вероятности
, называется равномерным, если ее плотность вероятности 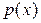 на этом отрезке постоянна, а вне его равна нулю, т.е.
на этом отрезке постоянна, а вне его равна нулю, т.е.
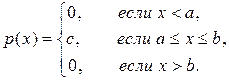
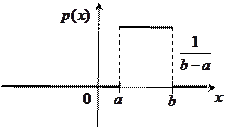 |
Отсюда
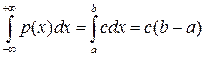 . Но
. Но 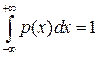 . Значит
. Значит 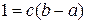 , откуда
, откуда 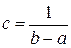 .
.
График функции 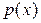 имеет вид:
имеет вид:
Определим интегральную функцию распределения 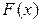 : если
: если 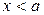 , то
, то 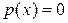 и, следовательно
и, следовательно 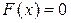 . Если
. Если 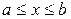 , то
, то 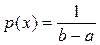 и
и 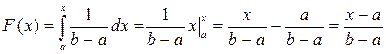 . Если
. Если 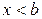 , то
, то 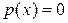 и
и 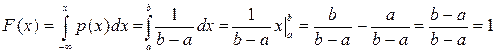 .
.
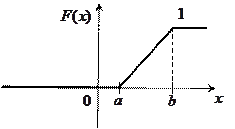 |
График функции
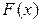 имеет вид:
имеет вид:
 2015-06-28
2015-06-28 365
365







