Пусть заданы две дискретные случайные величины Х и Y своими законам распределения:
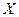
| -2 | и | 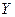
| -100 | ||||
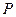
| 0,4 | 0,2 | 0,4 | 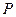
| 0,3 | 0,4 | 0,3 | |
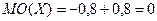
| 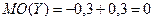
|
МО этих величин одинаковы, но возможные значения Х распределены значительно ближе к своему МО, чем значения Y.
Определение 1. Отклонением случайной величины Х от ее математического ожидания (или просто отклонение случайной величины) называется случайная величина 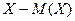 .
.
Теорема: математическое ожидание отклонения 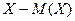 равно нулю.
равно нулю.
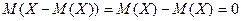 .
.
Эта теорема не дает возможности определить "степень рассеивания" величины Х. Такой характеристикой является квадрат отклонения случайной величины Х: 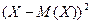 .
.
Закон распределения квадрата отклонения случайной величины Х запишем:
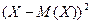
| 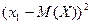
| 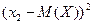
| … | 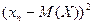
|
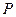
| 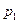
| 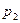
| … | 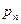
|
Определение 2. Дисперсией (dispersuis (лат.) – рассеянный; рассыпанный) дискретной случайной величины Х 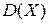 называется МО квадрата отклонения случайной величины Х от ее МО:
называется МО квадрата отклонения случайной величины Х от ее МО: 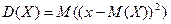 . Из закона распределения величины
. Из закона распределения величины 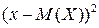 следует, что
следует, что
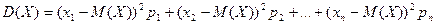
Свойства дисперсии дискретной случайной величины:
1. Дисперсия дискретной случайной величины 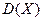 равна разности МО квадрата величины Х и квадрата ее МО:
равна разности МО квадрата величины Х и квадрата ее МО: 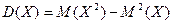 .
.
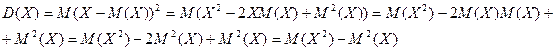
2. Дисперсия постоянной величины равна 0.
3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 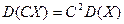 .
.
4. Дисперсия суммы двух независимых случайных величин равна суме дисперсий этих величин: 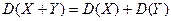 . Это свойство распространяется на сумму конечного числа слагаемых.
. Это свойство распространяется на сумму конечного числа слагаемых.
5. Дисперсия разности двух независимых случайных величин Х и Y равна сумме их дисперсий.
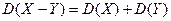 .
.
 2015-06-28
2015-06-28 534
534








