Определение. Средним квадратичным отклонением 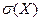 случайной величины Х называется корень квадратный из ее дисперсии:
случайной величины Х называется корень квадратный из ее дисперсии: 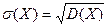 .
.
Пример. Случайна величина – число очков, которое выпало при однократном бросании кубика. Определим 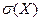 :
:
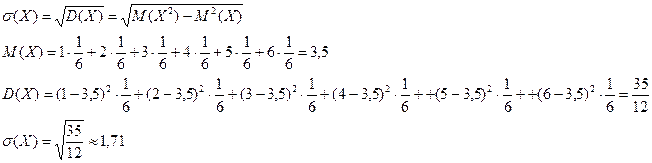
Ковариацией двух случайных величин 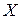 и
и 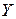 называется математическое ожидание произведения их отклонений от соответствующих математических ожиданий:
называется математическое ожидание произведения их отклонений от соответствующих математических ожиданий: 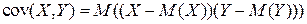 . Если ковариация равна нулю, то случайные величины
. Если ковариация равна нулю, то случайные величины 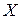 и
и 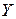 – независимы; для зависимых –
– независимы; для зависимых – 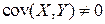 .
.
Коэффициентом корреляции 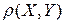 случайных величин
случайных величин 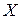 и
и 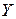 называется отношение их ковариаций к произведению средних квадратичных отклонений этих величин:
называется отношение их ковариаций к произведению средних квадратичных отклонений этих величин: 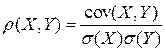 .
.
Свойства коэффициента корреляции:
1. 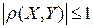 ;
;
2. если 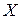 и
и 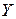 независимы, то
независимы, то 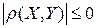 ;
;
3. если зависимость выражается формулой 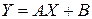 , то
, то 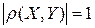 .
.
14.18. Системы двух случайных величин
и их числовые характеристики
Определение 1: упорядоченная пара 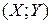 случайных величин
случайных величин 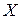 и
и 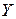 называется двухмерной случайной величиной или случайным вектором двухмерного пространства.
называется двухмерной случайной величиной или случайным вектором двухмерного пространства.
Двухмерная случайная величина 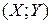 называется также системой случайных одномерных величин
называется также системой случайных одномерных величин 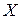 и
и 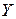 .
.
Определение 2: множество всех возможных значений дискретной двухмерной случайной величины с их вероятностями называется законом распределение этой случайной величины.
Дискретная двухмерная случайная величина считается заданной, если известен ее закон распределения: 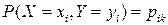 , где
, где 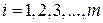 ,
, 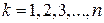 . Этот закон можно записать в виде таблицы с двойным входом:
. Этот закон можно записать в виде таблицы с двойным входом:
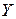
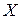
| 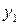
| 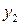
| 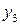
| 
| 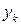
| 
| 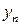
| ∑ |
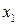
| 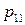
| 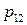
| 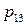
| 
| 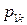
| 
| 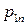
| 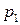
|
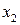
| 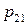
| 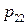
| 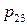
| 
| 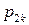
| 
| 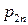
| 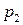
|

| 
| 
| 
| 
| 
| 
| 
| 
|
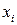
| 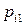
| 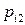
| 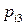
| 
| 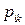
| 
| 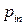
| 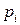
|

| 
| 
| 
| 
| 
| 
| 
| 
|
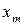
| 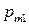
| 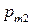
| 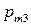
| 
| 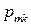
| 
| 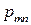
| 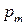
|
| ∑ | 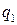
| 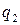
| 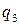
| 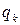
| 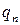
|
Так как события 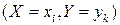 образуют полную группу событий, поэтому сумма всех вероятностей, указанных в таблице равна 1.
образуют полную группу событий, поэтому сумма всех вероятностей, указанных в таблице равна 1.
Определение 3: если для любой пары возможных значений 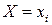 и
и 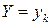 справедливо равенство
справедливо равенство 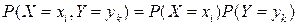 , то случайные величины называются независимыми. Это равенство есть необходимое и достаточное условие независимости случайных величин
, то случайные величины называются независимыми. Это равенство есть необходимое и достаточное условие независимости случайных величин 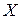 и
и 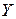 .
.
Определение 4: Зависимость математического ожидания случайной величины 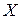 от значений других случайных величин называется регрессией. Зависимость между случайными величинами
от значений других случайных величин называется регрессией. Зависимость между случайными величинами 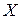 и
и 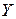 описывается прямой так:
описывается прямой так:
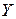 относительно
относительно 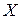 :
: 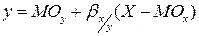 , где
, где 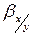 – коэффициент регрессии, равный
– коэффициент регрессии, равный 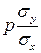 .
.
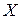 относительно
относительно 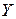 : прямой
: прямой 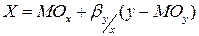 , где
, где 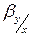 – коэффициент регрессии,
– коэффициент регрессии, 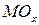 и
и 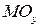 – математические ожидания.
– математические ожидания.
Коэффициент регрессии вычисляется по формуле 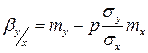 .
.
Литература
1. Баврин, И.И. Курс высшей математики: Учебник для студентов пед. ин-тов по спец. №2105 "Физика". – М.: Просвящение, 1992. – 400 с.
2. Гусак, А.А. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак, Е.А. Бричикова – 3-е изд., стереотип. – Мн.: ТетраСистемс. – 2001. – 640 с.
3. Метельский, Н.В. Дидактика математики. – Мн.: Из-во БГУ, 1975. – 256 с.
4. Микиша, А.М., Орлов, В.Б. Толковый математический словарь. Основные термины. – М.: Рус.яз., 1989. – 244 с.
 2015-06-28
2015-06-28 408
408








