Векторы. 1. Векторы: основные определения (скалярная величина, векторная величина, вектор, ноль-вектор, коллинеарные и компланарные векторы

1. Векторы: основные определения (скалярная величина, векторная величина, вектор, ноль-вектор, коллинеарные и компланарные векторы, равенство векторов, противоположные векторы, орт вектора, угол между векторами и вектором и осью, проекция вектора на ось, координаты, направляющие углы и косинусы вектора, модуль вектора). Формулы, связывающие основные понятия для векторов.

Пример. Вычислить направляющие косинусы вектора 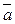={12;-15;-16}.

2. Линейные операции над векторами. Необходимый и достаточный признак коллинеарности векторов.

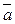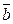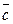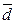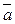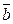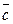Пример. Даны векторы: ={3;-2;6}; ={-2;1;0}; ={-3;0;9}. Найти вектор: =2 - + /3.

Решить эту же задачу графически, задав самостоятельно на плоскости векторы , , .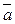

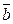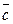3. Линейно зависимые и линейно независимые векторы. Теоремы о линейно зависимых и независимых векторах. Базис на плоскости и в пространстве. Разложение вектора по базису.

Пример. Разложить вектор 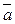={9;4} по базису 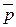и 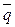, если 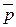={2;-3}; 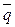={1;2}.

4. Тройка векторов. Правые и левые тройки векторов. Правила определения направленности тройки. Привести три примера различных троек, указав какие они. Деление отрезка в данном отношении.

Пример. Даны точки: А (-1;8;3) и В (9;-7;-2). Найти координаты точки С, если она делит отрезок АВ в отношении 1/4.

5. Скалярное произведение векторов и его свойства. Угол между двумя векторами. Физический смысл скалярного произведения.

Пример. При каком значении m вектор 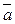={2;3;-1} перпендикулярен вектору 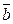={1;-5;m}.

6. Векторное произведение векторов и его свойства. Геометрический смысл векторного произведения.

Пример. Найти вектор 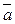x 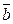и его модуль, если вектор 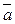={2;3;-1}, а вектор 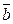={3;-1;-4}.

7. Смешанное произведение векторов и его свойства. Геометрический смысл смешанного произведения. Условие компланарности трех векторов.

Пример. Вычислить объем пирамиды с вершинами в точках: О (0;0;0); А (5;2;0); В (2;5;0); С (1;2;4).