Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Итак, пусть дана матричная игра с матрицей А порядка m хn. Согласно свойству 7 оптимальные смешанные стратегии х = (х1,..., хm), y = (y1,..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.
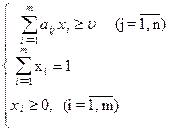
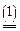

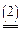
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения:
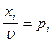
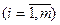 ,
, 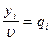
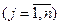 ,
,
Тогда (1) и (2) перепишется в виде:
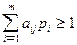 ,
, 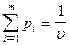 ,
, 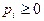 ,
, 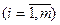 ,
,
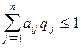 ,
, 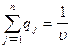 ,
, 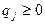 ,
, 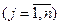 .
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi, чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi 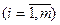 , при которых
, при которых
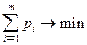 ,
, 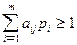 .
. 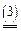
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, 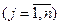 , при которых
, при которых
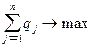 ,
, 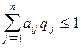 .
. 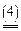
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi 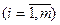 , qj
, qj 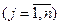 и u. Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
и u. Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
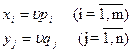
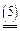
Пример. Найти решение игры, определяемой матрицей.
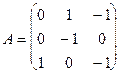
Решение. При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу
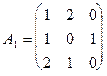
Составим теперь пару взаимно-двойственных задач:
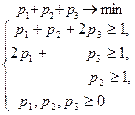
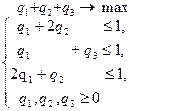
Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
| -1 | -1 | -1 | -3 | ||||||
| q4 | — | ||||||||
| q5 | 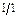
| ||||||||
| q6 | — |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
| -1 | |||||||||
| q4 | 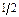
| ||||||||
| q3 | — | ||||||||
| q6 | 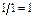
|
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
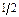
| 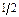
| 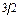
| 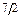
| ||||||
| q2 | 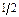
| 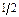
| 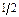
| 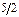
| |||||
| q3 | |||||||||
| q6 | 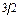
| 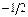
| 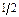
| 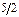
|
Из оптимальной симплекс-таблицы следует, что 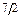
(q1, q2, q3) = (0; 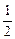 ; 1),
; 1),
а из соотношений двойственности следует, что
(p1, p2, p3) = (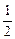 ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
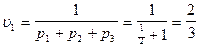 .
. 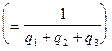 ,
,
а игры с платёжной матрицей А:
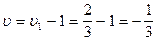 .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = 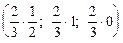 =
= 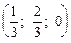
Y = (y1, y2, y3) = (uq1; uq2; uq3) = 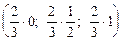 =
= 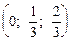 .
.
Варианты заданий для заочников по дисциплине «Исследование операций».
Вариант 1.
1.Нелинейное программирование. Области применения. Методы решения задач нелинейного программирования.
2.Постановка задач теории игр.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 2.
1. Постановка и решение задач нелинейного программирования.
2. Матричная игра стратегия игры. Примеры игр.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 3.
1.Элементы классической теории оптимизации. Функция Лагранжа. Множители Лагранжа.
2. Решение матричных игр. Смешанные стратегии. Чистые стратегии.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 4.
1. Динамическое программирование. Принцип оптимальности Беллмана.
2. Платежная матрица. Теорема Шепли-Сноу. Принцип доминирования.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 5.
1. Методы сетевого планирования и управления. Элементы сетевого графика.
2. Приближенное численное решение игр. Метод Брауна.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 6.
1. Временные параметры сетевого графика. Ранний и поздний сроки наступления событий. Работа, полный резерв времени, свободный резерв времени.
2. Игры с природой. Оптимальный критерий, критерии Сэвиджа, Лапласа.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 7.
1. Распределение ограниченных ресурсов. Последовательный метод.
2. Игры с природой. Критерии Гурвица, Вальда.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 8.
1. Параллельный метод распределения ограниченных ресурсов.
2. Формализация понятия игры.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 9.
1. Метод множителей Лагранжа. Функции и множители Лагранжа. Теорема Куна-Таккера.
2. Решение игр. Геометрическая интерпретация функции выигрыша.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 10.
1.Метод прямого поиска в задачах нелинейного программирования. Метод Хука-Дживса. Метод деформируемого симплекса.
2. Решение матричных игр. Принцип доминирования. Понижение порядка игры.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 11.
1. Решение задач нелинейного программирования. Оптимизация при наличии ограничений.
2. Решение матричных игр. Связь между матричными играми и линейным программированием.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 12.
1. Задачи нелинейного программирования. Методы непрямого поиска.
2. Решение задач теории игр в чистых стратегиях.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 13.
1. Градиентные методы решения задач нелинейного программирования.
2. Решения матричных игр в чистых стратегиях. Понижение порядка игры и решение ее.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 14.
1. Методы второго порядка для решения задач нелинейного программирования.
2. Принцип доминирования в решении матричных игр. Примеры.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 15.
1. Решение задач нелинейного программирования с ограничениями.
2. Решение задач теории игр графическим методом.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 16.
1. Принципы динамического программирования. Принцип оптимальности.
2. Минимаксный критерий в решении игр с природой.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 17.
1. Задача управления запасами предприятия.
2. Постановка задач теории игр. Матричные игры.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 18.
1. Математическая модель задачи управления запасами.
2. Решение матричных игр в чистых стратегиях.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 19.
1. Задача распределения ограниченных ресурсов.
2. Решение задач теории игр в смешанных стратегиях.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 20.
1. Пример решения задач оптимального распределения ресурсов.
2. Решение задач теории игр методами линейного программирования
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 21.
1. Задачи динамического программирования. Задача оптимальной замены оборудования.
2. Приближенное решение матричных игр. Метод Брауна.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 22.
1. Задача о загрузке в решении задач нелинейного программирования.
2. Решение матричных игр различными методами.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 23.
1. Методы сетевого планирования. Элементы сетевого графика.
2. Критерии Вальда, Гурвица в задачах игры с природой.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 24.
1. Задача управления запасами предприятия.
2. Постановка задач теории игр. Матричные игры.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Вариант 25.
1. Сетевые методы в решении задач распределении ограниченных ресурсов.
2. Матричная игра решение матричных игр в смешанных стратегиях.
3. Задача 1.
4. Задача 2.
5. Задача 3.
Задачи
1) Найти верхнюю и нижнюю цену игры и проверить наличие седловой точки
1) 2)
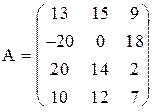
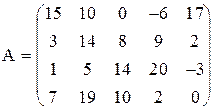
3) 4)
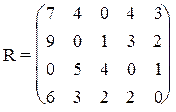
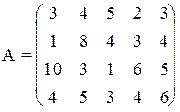
5) 6)
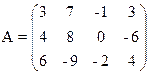
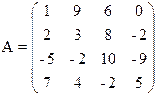
7) 8)
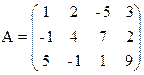
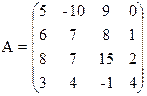
9) 10)
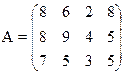
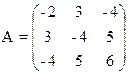
11) 12)
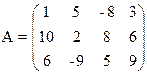
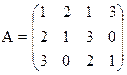
13) 14)
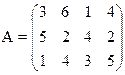
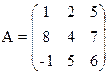
15) 16)
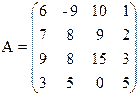
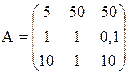
17) 18)
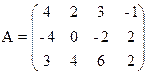
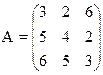
19) 20)
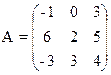
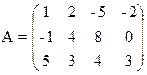
21) 22)
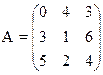
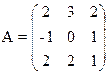
23) 24)
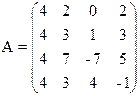
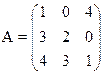
25)
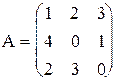
2) Решить игру графически
1) 2)
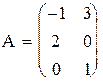
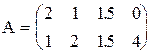
3) 4)
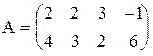
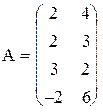
5) 6)
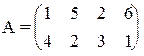
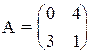
7) 8)
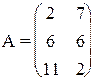
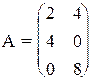
9) 10)
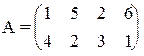
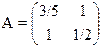
11) 12)
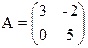
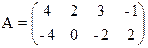
13) 14)
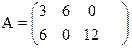
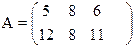
15) 16)
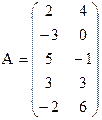
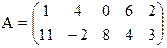
17) 18)
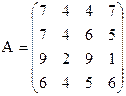
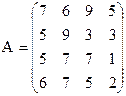
19) 20)
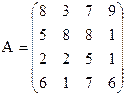
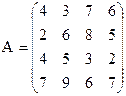
21) 22)
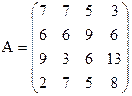
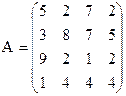
23) 24)
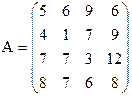
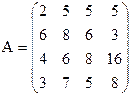
25)
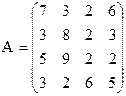
Решить игру симплекс-методом
1) 2)
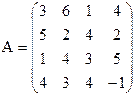
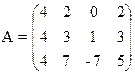
3) 4)
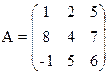
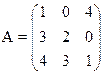
5) 6)
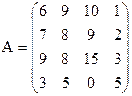
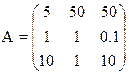
7) 8)
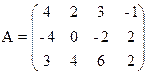
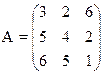
9) 10)
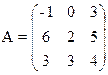

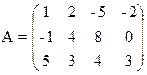
11) 12)
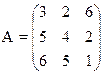
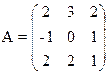
13) 14)
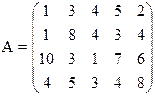
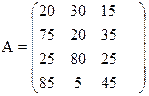
15) 16)
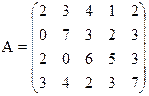
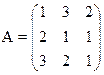
17) 18)
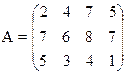
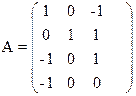
19) 20)
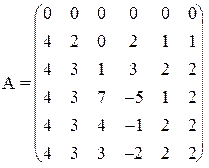
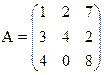
21) 22)
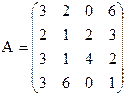
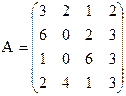
23) 24)
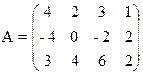
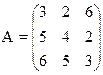
24)
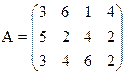
 2015-06-28
2015-06-28 595
595







