Модель динамики популяций с возрастной структурой П. Лесли

Пусть x_i (k), где 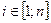– численность особей популяции в i -й возрастной группе в дискретные моменты времени k. Процессы размножения, гибели и перехода особей из одной возрастной группы в другую могут быть формализованы следующим образом (Розенберг, 1984). Первоначально установим, каким образом состояние популяции в момент времени k + 1 зависит от состояния в момент времени k. Численность первой группы (k = 1) представляет собой число новорожденных потомков всех остальных групп за единичный интервал времени; считается, что особи некоторой возрастной группы производят потомков прямо пропорционально численности особей в этой группе:

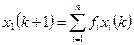, [1]

где f_i – коэффициент рождаемости i -й возрастной группы. Если обозначить через d_j <1 коэффициент выживаемости при переходе от возрастной группы j к группе j + 1, то можно записать n – 1 соотношение типа:

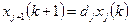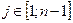, где [2]

Тогда, объединяя [1] и [2], можно записать систему n разностных уравнений, представляющих собой дискретную модель возрастного состава популяции. В матричной форме имеем:

x (k + 1) = Lx (k), [3]

где x (k) = { x_i (k)} – вектор численности отдельных возрастных групп, а

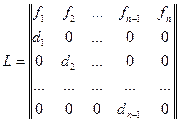– матрица коэффициентов рождаемости и выживаемости [4]

Если расписать подробнее, то получим:

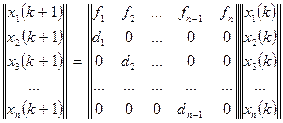
Крайний левый вектор-столбец отражает количество особей разных возрастных групп в момент времени k +1, а крайний правый вектор-столбец – количество особей разных возрастных групп в момент времени k. Матрица коэффициентов рождаемости и выживаемости есть матрица перехода из одного состояния в другое.

Для вычисления возрастного состава популяции в любой момент времени используем простые соотношения:

x (k + 1) = Lx (k)

x (k + 2) = Lx (k+1) = LLx (k) = L ² x (k)

x (k+m) = L ^m x (k)

Данная модель известна как модель Лесли (Leslie, 1945).

Квадратная матрица L является неотрицательной (все ее элементы неотрицательны). Для того чтобы матрица Лесли была неразложима (т.е. никакой перестановкой строк и соответствующих столбцов она не могла быть приведена к виду:

,

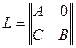где A и B – квадратные подматрицы), необходимо и достаточно, чтобы 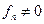. Биологически это условие означает, что в качестве n выступает не максимально возможный, а наибольший репродуктивный возраст особей.

Характеристическое уравнение системы [3] имеет следующий вид:

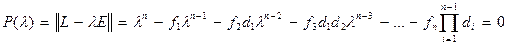, [5]

где E – матрица с единицами на главной диагонали, а все остальные ее члены равны нулю.

Так как матрица Лесли неотрицательна и неразложима, то в соответствии с теоремой Перрона-Фробениуса характеристическое уравнение имеет действительное положительное характеристическое число (максимальное среди всех остальных характеристических чисел), являющееся простым корнем этого уравнения. Кроме того, так как 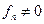, то уравнение [5] не имеет нулевых корней. Из этих условий следует, что асимптотическое решение системы [3] для достаточно больших k будет определяться собственным числом λ₁ (максимальным из всех) и соответствующим ему собственным вектором b ₁ матрицы Лесли:

,

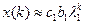где с ₁ – некоторая постоянная, зависящая от координат начального распределения вектора x (0).

Если λ₁>1, то популяция растет (x (k) увеличивается с ростом k). Если λ₁<1, то популяция гибнет. Наконец, если λ₁=1, то общая численность популяции асимптотически стремиться к постоянной величине. P (1)<0 эквивалентно выражению λ₁>1, т.е. условию роста популяции (см. формулу 5), аналогично P (1)>0 соответствует гибели, а P (1) = 0 – стационарной численности популяции. Таким образом, по виду матрицы [4] без определения собственного значения λ₁ можно делать качественные выводы о характере моделируемой популяции во времени.

Недостаток модели Лесли аналогичен недостатку модели Мальтуса – это неограниченный рост популяции при λ₁>1, что соответствует лишь начальным фазам роста некоторых популяций (Розенберг, 1984).

Модель Лесли была использована для описания возрастной структуры ценопопуляции овсеца Шелля (Helictotrichon schellianum). Это рыхлокустовой мелкодерновинный злак северных луговых степей. А.Н. Чебураева (1977) исследовала распределение численности особей этого злака по возрастным группам в Попереченской степи Пензенской области на водораздельном плато на общей площади 50 м² в различные годы (1970-1974 гг.). Ежегодно учеты особей овсеца проводились на 200 площадках 0,5×0,5 м. Такая большая повторность наблюдений позволяет считать полученные оценки численности особей в каждой возрастной группе достаточно устойчивыми. Исследователем было выделено девять возрастных групп:

· проростки и всходы

· прегенеративные особи (ювенильные, имматурные и молодые вегетативные)

· генеративные особи (молодые, зрелые и старые)

· постгенеративные особи (субсенильные и сенильные)

Чтобы учесть влияние погодных условий на динамику ценопопуляции овсеца Шелля (1972 год – год засухи), необходимо перейти от абсолютных значений численности к относительным. При равных интервалах для каждой возрастной группы должно выполняться соотношение x_{i+ 1}(k + 1) < x _i(k), т.е. в последующий момент времени в более старшей возрастной группе не должно быть больше особей, чем их было в настоящий момент времени в более молодой группе. В связи с этим первые семь возрастных классов А.Н. Чебураевой были объединены. Исходные данные для построения модели приведены в табл. 1.

Таблица 1

Абсолютная и относительная численности ценопопуляции овсеца Шелля для различных возрастных групп (по данным А.Н. Чебураевой, 1977)

Год	Проростки, прегенеративные и генеративные особи	Постгенеративные особи	Общая численность
субсенильные	сенильные
абсолютные	%	абсолютные	%	абсолютные	%

Несмотря на модификацию, данные за 1972 год все же отличаются от других, поэтому от модели Лесли не следует ожидать точного прогноза относительно численности. Чтобы получить более точный прогноз, коэффициенты матрицы Лесли должны быть поставлены в зависимость от погодных условий.

Для построения матрицы L используем некоторые представления о возможных значениях ее коэффициентов. Так, коэффициенты рождаемости f_i при переходе от первой группы, включающей все генеративные состояния, к более старым растениям должны уменьшаться. Коэффициенты выживаемости d_i взяты примерно равными (из первой группы во вторую переходит половина особей, из второй в последующую – несколько меньше). Окончательно, матрица Лесли имеет следующий вид:

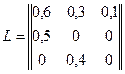
Характеристическое уравнение для модели Лесли в данном случае представляет собой полином третьей степени:

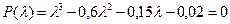
Легко убедиться, что P (1) = 0,23>0 по теории П. Лесли указывает на старение и увядание данной ценопопуляции в наблюдаемом интервале времени.

Вычислим корни характеристического уравнения. Для этого воспользуемся формулой Кардано. Рассмотрим алгоритм решения кубического уравнения вида:

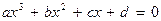[6]

Произведем замену:

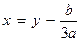
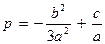
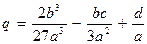
Получим уравнение:

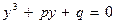[7]

Предположим, что значение корня представляется в виде суммы двух величин y = α + β, тогда уравнение [7] примет вид:

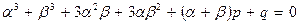
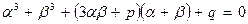[8]

Приравняем к нулю выражение (3 αβ + p), тогда от уравнения [8] можно перейти к системе:

,

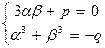которая равносильна системе:

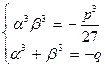
Мы получили формулы Виета для двух корней квадратного уравнения (α ³ – первый корень; β ³ – второй корень). Отсюда:

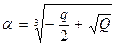
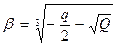
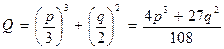
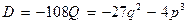– дискриминант уравнения [7].

Если D>0, тогда уравнение имеет три различных вещественных корня.

Если D = 0, то хотя бы два корня совпадают: либо уравнение имеет двойной вещественный корень и еще один, отличный от них вещественный корень, либо все три корня совпадают, образуя корень кратности три.

Если D<0, то уравнение имеет один вещественный и пару комплексно-сопряженных корней.

Таким образом, корни кубического уравнения в канонической форме равны:

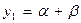
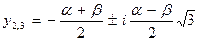, где i = 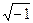– мнимое число.

Применять эту формулу нужно для каждого значения кубического корня 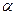(кубический корень всегда дает три значения!) и брать то значение корня 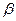, чтобы выполнялось условие: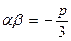

Для проверки можно использовать следующие соотношения:

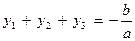
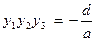
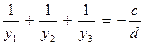, где d ≠ 0

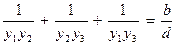, где d ≠ 0

Окончательно:

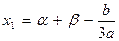
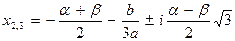
В нашем случае: a = 1; b = –0,6; c = –0,15; d = –0,02;

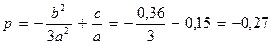
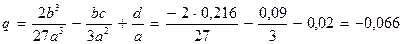
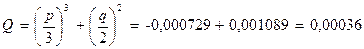
D = – 0,03888, D <0. Уравнение имеет один вещественный и пару комплексно-сопряженных корней.

Далее по приведенным выше формулам находим собственные значения характеристического уравнения: λ₁ = 0,814; λ₂ = – 0,107 + 0,112 i; λ₃ = – 0,107 – 0,112 i, где i = 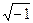– мнимое число. Таким образом, характеристическое уравнение имеет один действительный и два комплексных корня. λ₁ является максимальным корнем этого уравнения, а так как λ₁<1, то вывод об увядании данной ценопопуляции остается без изменения.

Кроме того, согласно Ю.М. Свиржеву и Д.О. Логофету (1978) простым и достаточным условием для существования периодических колебаний общей численности служат выражения:

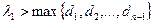
или

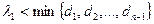
В связи с этим следует ожидать существование периодических колебаний численности ценопопуляции овсеца Шелля, так как λ₁>max (0,5; 0,4).

В рамках модели Лесли объясняются наблюдавшиеся А.Н. Чебураевой явления – старение ценопопуляции овсеца и наличие колебаний в распределении особей по возрастному спектру в течение ряда лет. На рис. 1 показана динамика численности особей для каждой из выделенных возрастных групп. Для того, чтобы модель давала удовлетворительный прогноз, необходимо, чтобы коэффициенты матрицы L были не постоянными, а зависимыми от погодных условий. Если дополнить модель Лесли условиями нормировки получаемого вектора x (k +1) так, чтобы сумма численности всей популяции равнялась наблюдаемой общей численности в момент времени k +1, то тем самым косвенно учитывается влияние погодных условий. Модель в этом случае будет иметь следующий вид:

x (k +1) = Lx (k), ,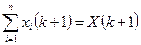

где X (k +1) – общая численность популяции в момент времени k +1 (остальные обозначения аналогичны модели Лесли). Таким образом, зная общую численность особей данной ценопопуляции в различные годы, построив матрицу Лесли из общебиологических соображений и взяв в качестве x (1) распределение особей овсеца по возрастным группам в 1970 г., можно достаточно правдоподобно восстановить распределение особей по возрастным группам в другие годы.

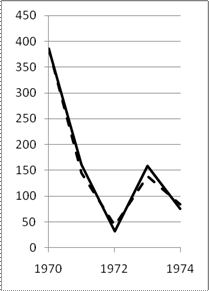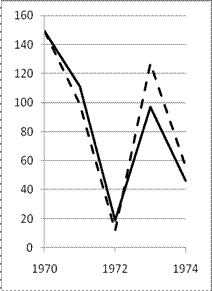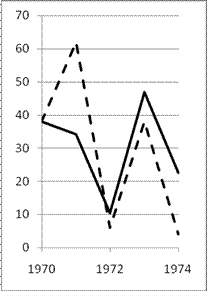Проростки, прегенеративные и генеративные особи	Субсенильные особи	Сенильные особи
Рис. 1 Динамика абсолютной численности ценопопуляции Helictotrichon schellianum для различных возрастных групп. Сплошная линия – эмпирические данные, пунктир – прогноз по модели Лесли с поправкой на общую численность по эмпирическим данным. Ось ординат – абсолютная численность, ось абсцисс - годы.

Расчет абсолютной численности ценопопуляции Helictotrichon schellianum для различных возрастных групп в различные годы производится следующим образом. Берем исходные данные за 1970 год и подставляем их в матрицу. Производим умножение матриц по соответствующим правилам. Получаем новую матрицу со значениями численности различных возрастных групп за 1971 год.

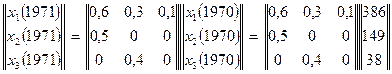
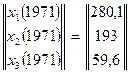
Так повторяем каждый раз для каждого года. Результаты заносим в таблицу, вычисляем общую численность особей по модели Лесли, соотносим ее с эмпирическими данными. Далее вносим поправочный коэффициент и приводим в соответствие общей численностью расчеты по модели (табл. 2).

Таблица 2

Абсолютная численность ценопопуляции овсеца Шелля для различных возрастных групп по модели Лесли и эмпирическим данным

Возрастная группа
эмпирические данные	модель Лесли	эмпирические данные	модель Лесли	модель Лесли с поправкой на общую численность	эмпирические данные	модель Лесли	модель Лесли с поправкой на общую численность	эмпирические данные	модель Лесли	модель Лесли с поправкой на общую численность	эмпирические данные	модель Лесли	модель Лесли с поправкой на общую численность
Проростки, прегенеративные и генеративные особи				280,1	160,9		231,9	31,5		188,9	158,1		153,7	75,1
Субсенильные особи				193,0	110,9		140,1	19,0		116,0	97,1		94,5	46,2
Сенильные особи				59,6	34,2		77,2	10,5		56,0	46,9		46,4	22,7
Общая численность				532,7			449,2			360,9			294,6