Переменной

Нам даны матрица 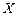размерности 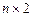и вектор-столбец 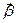(его координатами являются искомые коэффициенты a, b):

, .

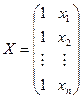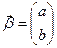Покажем, что

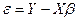(3).

В самом деле,

,

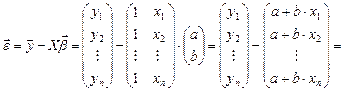
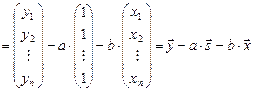где .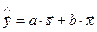

В данном случае условие 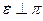означает, что

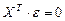(4).

Тогда получим:

,

,

.

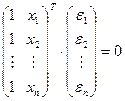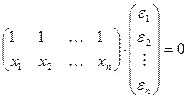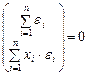Так же заметим, что (2) и (4) эквивалентны.

Задача МНК сводится к нахождению 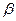из системы уравнений (3) и (4):

.

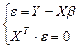Подставим (3) в (4), получим:

.

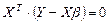
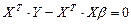
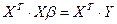Из полученного уравнения нам надо выразить матрицу 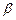. Так как для матриц нет операции деления, домножим обе части:

.

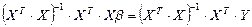Примечание. Нахождение обратной матрицы.

Пусть 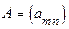— матрица размерности 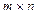. Тогда матрица 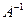называется обратной к матрице 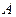и вычисляется следующим образом:

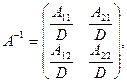
где 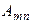— алгебраическое дополнение элемента 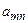, умноженное на ,

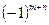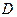— определитель матрицы .

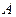Алгебраическое дополнение получается вычеркиванием m -строки и n -столбца.

Обратная матрица существует, если детерминант исходной не равен нулю.

Так как результатом умножения матрицы на обратную является единичная матрица, то

.

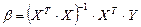Примечание. Результат получен для нецентрированных и ненормированных данных.

Покажем, что векторная запись коэффициентов a, b эквивалентна полученным ранее выражениям в координатной записи.

Вычислим 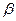по уравнению:

, ,

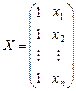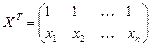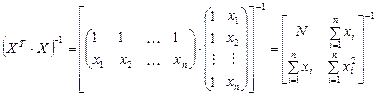
Для построения обратной матрицы, рассчитаем детерминант исходной :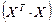

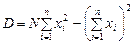, получим обратную матрицу:

,

,

,

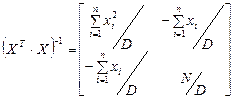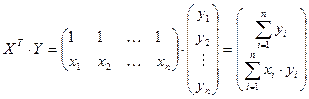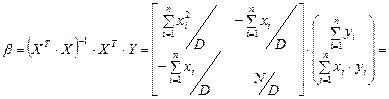
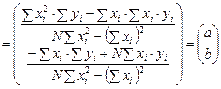то есть:

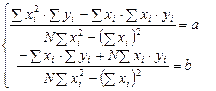. (5)

Покажем, что выражения для компонент вектора b соответствуют выражениям для коэффициентов a и b, полученных из системы нормальных уравнений (см. п. 3.6).

В п. 3.6 было получено:

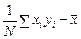
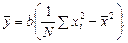
После использования определения среднего и домножения на 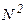для коэффициента b имеем:

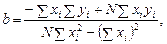(6)

что соответствует второй компоненте вектора b (5).

Для коэффициента a с учетом (6) имеем:

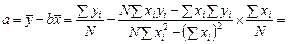
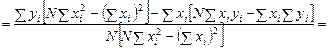
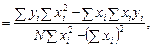
что соответствует первой компоненте вектора b (5).