2015-06-28
1569
Определение 1. Производной скалярной функции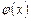 
от векторного аргумента 
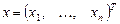размерности 
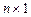называется вектор-строка размерности 
:
.
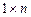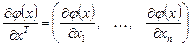Определение 2. Производной векторной функции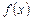 
размерности 
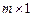от векторного аргумента 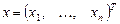размерности 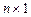называется матрица размерности 
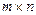, составленная из производных (матрица Якоби):
.
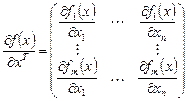При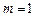 
определение 2 переходит в определение 1.
Правила дифференцирования по векторному аргументу
1. Пусть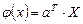 
, при этом
.
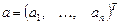
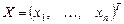Заметим, что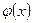 
— скаляр. В самом деле, размерность 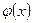найдем с учетом размерности 
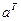и X:
.
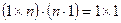Тогда
.
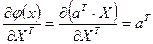2. Пусть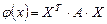 
— скалярная функция, 
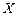— матрица 
, 
— 
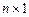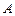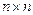. Тогда:
.
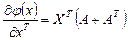Для нахождения минимума функции (9) по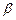 
, возьмем производную по .
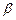Производная от суммы — есть сумма производных. Производная от первого члена будет нуль (т.к. от 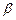не зависит); производную от второго члена найдем, используя правило 1 и равенство (8), где 
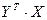играет роль :
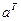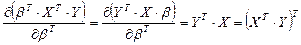; (10)
производная от третьего члена с использованием правила 2, где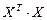 
играет роль А:
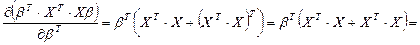
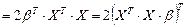. (11)
Дифференцируя (9) по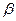 
, с учетом (10) и (11) получим:
.
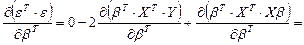
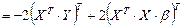Для нахождения минимума функции по 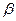полученный результат приравняем к нулю:
.
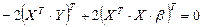Далее находим :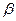
.
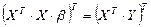
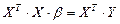
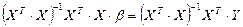
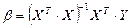Полученный результат и есть решение по обычному методу наименьших квадратов (OLS, Ordinary Least Squares Method).
