Необходимые условия экстремума и его геометрическая интерпретация
Рассмотрим 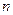 — мерное пространство векторов
— мерное пространство векторов 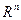 , в котором определено скалярное произведение
, в котором определено скалярное произведение 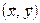 , где
, где
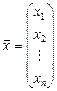 ,
, 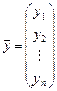 .
.
Поскольку вектор можно рассматривать как матрицу размерности 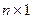 , то для обозначения матриц данной размерности будем применять соответствующие буквенные обозначения векторов без стрелки над буквой, например:
, то для обозначения матриц данной размерности будем применять соответствующие буквенные обозначения векторов без стрелки над буквой, например: 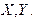
Тогда скалярное произведение 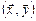 выглядит следующим образом:
выглядит следующим образом:
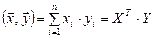 .
.
Пусть 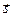 — единичный вектор, а
— единичный вектор, а 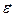 — вектор ошибок:
— вектор ошибок:
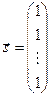 ,
, 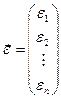 .
.
Тогда регрессионная прямая имеет вид:
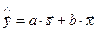 (1)
(1)
В самом деле, для каждого 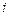 -го наблюдения имеем:
-го наблюдения имеем:
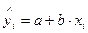 , (
, (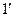 )
)
тогда для всех 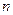 наблюдений:
наблюдений:
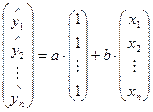 ,
,
что является развернутой формулой уравнения (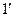 ).
).
Геометрическая интерпретация уравнения (1): вектор 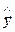 лежит в плоскости
лежит в плоскости 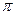 , натянутой на вектора
, натянутой на вектора 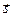 и
и 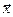 . Проиллюстрируем расположение вектора
. Проиллюстрируем расположение вектора 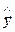 на плоскости
на плоскости 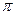 (рис. 3.5).
(рис. 3.5).
| 
|
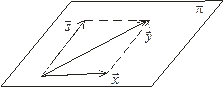
Рис. 3.5 Расположение вектора 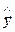 в плоскости
в плоскости 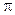 . .
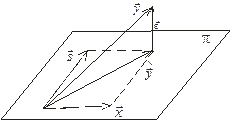
| Рис. 3.6 Аппроксимация вектора 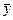 вектором вектором 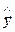 . .
|
Это есть геометрическая интерпретация задачи МНК:
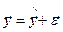 ,
, 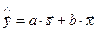
Задача МНК состоит в том, чтобы найти такие a, b, чтобы длина вектора 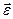 была минимальной:
была минимальной:
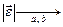 min.
min.
Геометрически задачу МНК можно сформулировать так: найти наилучшую аппроксимацию вектора 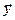 вектором
вектором 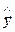 , лежащим в плоскости
, лежащим в плоскости 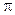 (рис. 3.6). Для этого необходимо и достаточно, чтобы вектор
(рис. 3.6). Для этого необходимо и достаточно, чтобы вектор 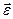 был перпендикулярен плоскости
был перпендикулярен плоскости 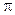 .
.
Запишем это с использованием матричных обозначений:
Если 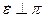 , то он перпендикулярен любому вектору с плоскости
, то он перпендикулярен любому вектору с плоскости 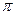 , значит
, значит 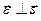 и
и 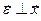 . Если векторы перпендикулярны, то их скалярное произведение равно нулю:
. Если векторы перпендикулярны, то их скалярное произведение равно нулю:
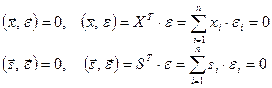 ,
,
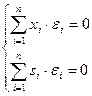 (2).
(2).
Система (2) является системой нормальных уравнений, полученной в п. 3.6.
 2015-06-28
2015-06-28 265
265







