Исходная модель в компонентном виде:
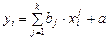 , для
, для 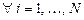 .
.
Введем обозначения:
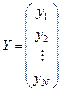 — вектор объясняемой переменной y размерности
— вектор объясняемой переменной y размерности 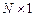 ,
,
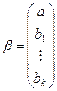 — вектор коэффициентов размерности
— вектор коэффициентов размерности 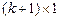 ,
,
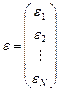 — вектор ошибок размерности
— вектор ошибок размерности 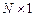 ,
,
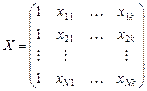 — матрица объясняющих переменных размерности
— матрица объясняющих переменных размерности 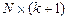 ,
,
тогда
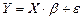 ,
,
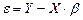 (7).
(7).
Вектор решений 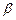 находится путем минимизации квадрата длины вектора остатков
находится путем минимизации квадрата длины вектора остатков 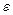 :
:
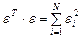 .
.
Учитывая свойства транспонированных матриц, получим:
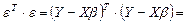
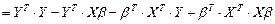 .
.
Здесь было учтено:
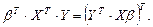
Примечание. Правило транспонирования матриц.
При транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке.
Например:
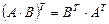
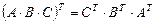
Покажем, что выполняется:
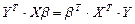 (8),
(8),
Для умножения матриц 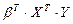 , проверим их размерность. Получим:
, проверим их размерность. Получим:
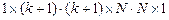 ,
,
по правилам перемножения матриц, итогом произведения будет скаляр — матрица размерности 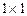 . Поскольку матрица
. Поскольку матрица 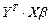 — тоже скаляр, а скаляр не меняется при транспонировании, то
— тоже скаляр, а скаляр не меняется при транспонировании, то
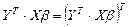 , а значит,
, а значит,
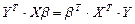 .
.
Итак:
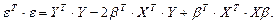 (9)
(9)
Чтобы найти минимум суммы квадратов остатков (минимальную длину вектора 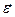 ), продифференцируем данную функцию по
), продифференцируем данную функцию по 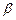 .
.
 2015-06-28
2015-06-28 350
350








