Пусть планируется эксплуатировать оборудование в течение некоторого периода времени продолжительностью n лет. Оборудование имеет тенденцию с течением времени стареть и приносить все меньший доход r(t). При этом возможность в начале любого года продать устаревшее оборудование за цену S(t) и купить новое оборудование за цену P. Под возрастом оборудования понимают период эксплуатации оборудования после последней замены, определенных в годах.
Требуется найти оптимальный план замены оборудования с тем, чтобы суммарный доход за все n лет был бы наибольшим, учитывая, что к началу эксплуатации возраст оборудования составляет t0 лет.
Исходными данными в задаче является доход r(t) от эксплуатации в течении одного года оборудования возраста t лет, остаточная стоимость S(t), цена нового оборудования P и начальный возраст оборудования t0.
| t | … | n | ||
| r | r(0) | r(1) | … | |
| S | S(0) | S(1) | … | S(n) |
Очевидно, что доход от эксплуатации оборудования за годы с k по n года будет зависеть от возраста оборудования к началу рассматриваемого шага.
Переменной управления на каждом шаге является логическая переменная, которая может принимать одно из двух значений:
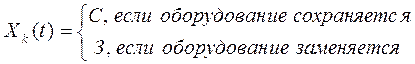
Функцию Беллмана Fk(t) определяют как максимально возможный доход от эксплуатации оборудования за годы с к по n, если к началу каждого возраст оборудования составлял t лет:
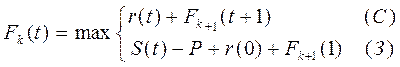
Для k = n 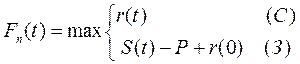 .
.
В результате безусловной оптимизации определяются годы, вначале которых следует произвести замену оборудования.
Пример 33. Найти оптимальную стратегию эксплуатации оборудования на период 6 лет, если годовой доход и остаточная стоимость S(t) в зависимости от возраста заданы в таблице. Стоимость нового оборудования P = 13, а возраст оборудования к началу эксплуатационного периода составлял один год.
| t | |||||||
| r(t) | |||||||
| S(t) |
Решение. Условная оптимизация.
k = 6.
| F6 | ||||||
| r(t) | ||||||
| S(t) – P + r(0) | -1 | |||||
| max | ||||||
| С/З | С | С | С | С | С | С |
Реализация в EXCEL приведена на рис. 23. Для подсчета последней строки используется команда:
ЕСЛИ(И(C13 = C11;C13 =C 12);"С/З";ЕСЛИ(C13 = C11;"С";"З"))
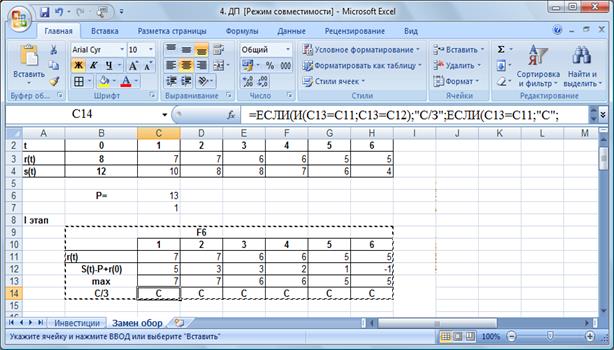
Рис. 23. Экранный вид первого шага
Аналогично строятся остальные шаги: k = 5
| F5 | |||||
| r(t) | |||||
| r + F6 | |||||
| S(t) – P + r(0) + F6(1) | |||||
| max | |||||
| С/З | С | С | С | С | С |
| F4 | ||||
| r(t) | ||||
| r + F5 | ||||
| S(t) – P + r(0) + F5(1) | ||||
| max | ||||
| С/З | С | С | С/З | С/З |
| F3 | |||
| r(t) | |||
| r + F4 | |||
| S(t) – P + r(0) + F4(1) | |||
| max | |||
| С/З | С | С | З |
| F2 | ||
| r(t) | ||
| r + F3 | ||
| S(t) – P + r(0) + F3(1) | ||
| max | ||
| С/З | С/З | С |
| F1 | r(t) | r + F2 | S(t) – P + r(0) + F2(1) | max | С/З |
| С |
Результаты сведены в таблице. В таблице выделено значение – замена оборудования
| k/t | ||||||
| 23 | ||||||
Безусловная оптимизация.
k = 1 и F1(1) = 37 с сохранением оборудования, следовательно к началу второго года возраст оборудования t2 = t1 + 1 = 2; k = 2, Х2(2) = с; k = 3, Х3(3) = з, т.е. необходимо заменить оборудование; k = 4, Х4(1) = с; k = 5, Х5(2) =с; k = 6, Х6(3) = с. Т.е., за 6 лет эксплуатации оборудования, замену нужно произвести один раз – в начале третьего года эксплуатации.
 2015-06-28
2015-06-28 3927
3927
