Рассмотрим три последовательных положения точки на траектории, соответствующие моментам времени 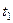 ,
, 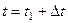 ,
, 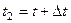 (рис. 2). Определим среднее ускорение на участке
(рис. 2). Определим среднее ускорение на участке 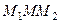 :
: 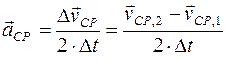 . Вектор среднего ускорения
. Вектор среднего ускорения
лежит в плоскости треугольника 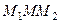 и направлен в сторону вогнутости траектории. Вектор мгновенного ускорения движущейся точки в положении М равен
и направлен в сторону вогнутости траектории. Вектор мгновенного ускорения движущейся точки в положении М равен 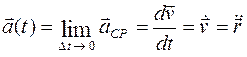 и лежит в соприкасающейся плоскости. Соприкасающуюся к траектории в точке М плоскость представим себе как предельное положение плоскости треугольника
и лежит в соприкасающейся плоскости. Соприкасающуюся к траектории в точке М плоскость представим себе как предельное положение плоскости треугольника 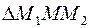 при условии
при условии 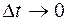 , т.е. при
, т.е. при 
1.1.7. Путь точки на заданном промежутке времени 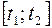
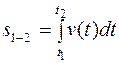 – длина пройденной дуги траектории.
– длина пройденной дуги траектории.
1.1.8. Исследовать траекторию точки при координатном способе задания ее движения бывает удобно, если исключить время как параметр из уравнений движения и составить таким способом уравнения траектории в виде зависимостей между координатами точки.
1.1.9. Скорость точки при задании ее движения в декартовой системе координат
Проекции скорости на оси координат:
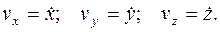
Составляющие скорости по осям координат:
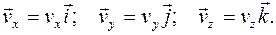
Вектор скорости: 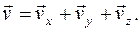
Величина (модуль вектора) скорости:
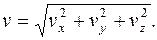
 2015-06-28
2015-06-28 630
630








