Кривизна кривой 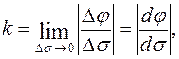 где
где 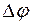 – угол поворота касательной к кривой на участке длиной
– угол поворота касательной к кривой на участке длиной 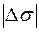 .
.
Радиус кривизны - величина, обратная величине кривизны: 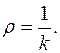
Радиус кривизны окружности есть радиус этой окружности; радиус кривизны прямой бесконечно велик. Радиус кривизны измеряется в метрах.
Точка нормали, отстоящая от данной точки траектории в направлении вогнутости кривой на расстояние 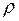 , называется центром кривизны кривой, соответствующим данной точке кривой. Геометрическое место центров кривизны образует линию - эволюту исходной кривой (evolutus (лат.)– развернутый; voluto – катать, катить). Исходная кривая является эвольвентой относительно своей эволюты (evolventis – разворачивающий).
, называется центром кривизны кривой, соответствующим данной точке кривой. Геометрическое место центров кривизны образует линию - эволюту исходной кривой (evolutus (лат.)– развернутый; voluto – катать, катить). Исходная кривая является эвольвентой относительно своей эволюты (evolventis – разворачивающий).
♦ Если аппроксимировать траекторию на участке 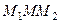 (рис. 2) дугой окружности, то её центр лежит в точке
(рис. 2) дугой окружности, то её центр лежит в точке 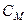 пересечения перпендикуляров, восстановленных из середин хорд
пересечения перпендикуляров, восстановленных из середин хорд 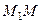 и
и 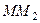 . Предельное положение точки
. Предельное положение точки 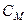 при условии
при условии 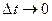 , когда
, когда 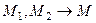 , есть центр кривизны траектории в точке М.
, есть центр кривизны траектории в точке М.
Если с катушки радиуса R сматывать нить, сохраняя отмотанную часть прямой, то конец нити опишет одну из эвольвент окружности, а именно, соответствующую той точке, с которой начал сматываться конец нити. На рис. 3,а изображена эвольвента окружности радиуса 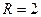 , соответствующая крайней правой начальной точке при сматывании нити против часовой стрелки. Параметрические уравнения этой эвольвенты
, соответствующая крайней правой начальной точке при сматывании нити против часовой стрелки. Параметрические уравнения этой эвольвенты
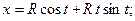
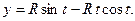
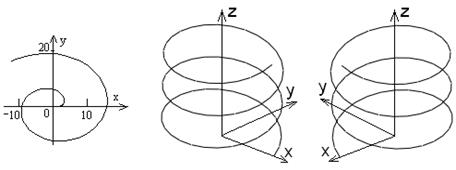
а б в
Рис. 3. Эвольвента окружности. Винтовые линии
При 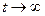 эта кривая приближается к спирали Архимеда, уравнение которой в полярных координатах
эта кривая приближается к спирали Архимеда, уравнение которой в полярных координатах 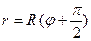 .
.
Зубцы колес большинства зубчатых передач имеют эвольвентный профиль, благодаря чему минимизируется скольжение зубца по зубцу и упрощается изготовление самих зубчатых колес. Основу профилей зубцов составляют эвольвенты («развертки») основных окружностей (см. «Теорию машин и механизмов») зацепляющихся колес.
1.1.15. Естественный трехгранник (натуральный триэдр) - трехгранник, построенный на осях касательной, нормали и бинормали. Орт бинормали определяется как 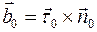 ; тогда
; тогда 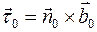 и
и 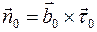 . Соприкасающаяся плоскость проходит через касательную и нормаль. Плоскость, содержащая нормаль и бинормаль, называется нормальной плоскостью, а плоскость, содержащая бинормаль и касательную, - спрямляющей. Естественный трехгранник ориентирован в пространстве соответственно форме кривой. Информация о форме (о внутренней геометрии кривой) может быть использована при исследовании движения материальной точки по данной кривой.
. Соприкасающаяся плоскость проходит через касательную и нормаль. Плоскость, содержащая нормаль и бинормаль, называется нормальной плоскостью, а плоскость, содержащая бинормаль и касательную, - спрямляющей. Естественный трехгранник ориентирован в пространстве соответственно форме кривой. Информация о форме (о внутренней геометрии кривой) может быть использована при исследовании движения материальной точки по данной кривой.
Пространственной кривая независимо от её расположения относительно окружающих предметов может быть описана путем задания в каждой точке 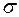 кривизны
кривизны 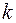 и кручения
и кручения 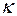 (греч. «каппа») кривой:
(греч. «каппа») кривой:
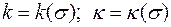 .
.
Величина кручения 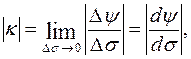 где
где 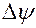 – угол поворота бинормали к кривой на участке длиной
– угол поворота бинормали к кривой на участке длиной 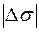 .
.
Имеют место формулы Серре – Френе:
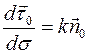 ;
; 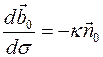 .
.
Кривизна – положительный параметр. Кручение «правой» винтовой линии, изображенной на рис. 3, б, положительно. Кручение «левой» (рис. 3, в) – отрицательно.
1.1.16. Равнопеременное движение точки определяется условием
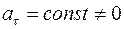 ; тогда имеют место формулы:
; тогда имеют место формулы:
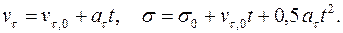
 2015-06-28
2015-06-28 13798
13798
