Скалярное произведение

Скалярным произведением векторов 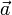и 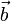называют число, равно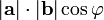е , где 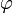— угол между векторам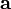и и 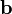. Обозначения: 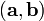или .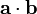

Если один из векторов является нулевым, то несмотря на то, что угол 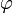не определён, произведение равно нулю.

Свойства скалярного произведения векторов:

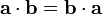1. — коммутативность.
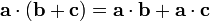2. — дистрибутивность.
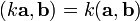3. — линейность по отношению к умножению на число.
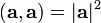4. — норма вектора (Квадрат вектора).

Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора 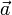с единичным вектором есть ортогональная проекция вектора 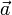на направление единичного вектора.