Произведение вектора н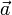а число

Произведением вектора и числа λ называется вектор, обозначаемы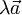й (или 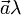), модуль которого равен , а направление совпадает с направлением вектора 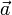, если 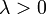, и противоположно ему, если 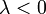. Если же 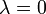, или вектор 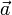нулевой, тогда и только тогда произведение 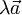— нулевой вектор.

• Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .

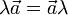Из определения произведения вектора на число легко вывести следующие свойства:

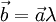1. если , то 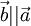. Наоборот, если 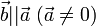, то при некотором λ верно равенство ;
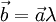2. всегда 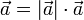°, то есть каждый вектор равен произведению его модуля на орт.