Практическое занятие № 3
«Операции над векторами. Вычисление модуля и скалярного произведения»
1. Цель: Выработать навыки и умения у студентов в решении задач на действия с
векторами
2. Пояснения к работе:
Краткие теоретические сведения
Определение вектора

 Вектором называется направленный отрезок. Вектор, заданный парой несовпадающих точек А и В, обозначается символом
Вектором называется направленный отрезок. Вектор, заданный парой несовпадающих точек А и В, обозначается символом 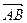 .Точка А называется началом, а точка В – концом вектора. Расстояние
.Точка А называется началом, а точка В – концом вектора. Расстояние 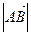 называется длиной (модулем) вектора
называется длиной (модулем) вектора 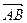 . Для обозначения векторов употребляются также строчные латинские буквы со стрелкой наверху:
. Для обозначения векторов употребляются также строчные латинские буквы со стрелкой наверху: 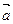 ,
, 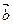 , …,
, …, 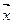 ,
, 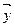 . Вектор
. Вектор 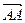 , концы которого совпадают, называется нулевым вектором. Длина нулевого вектора равна нулю. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два нулевых вектора
, концы которого совпадают, называется нулевым вектором. Длина нулевого вектора равна нулю. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два нулевых вектора 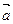 и
и 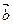 коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы
коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы 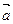 и
и 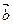 называются сонаправленными
называются сонаправленными 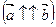 , во втором – противоположно направленными
, во втором – противоположно направленными 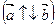 . Равные векторы сонаправлены и равны по модулю, т.е. если
. Равные векторы сонаправлены и равны по модулю, т.е. если 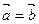 , то
, то 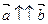 и
и 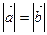 , и обратно, если векторы сонаправлены и равны по модулю, то она равны, т.е. если
, и обратно, если векторы сонаправлены и равны по модулю, то она равны, т.е. если 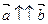 и
и 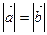 , то
, то 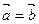 .
.
 2015-06-28
2015-06-28 300
300







