Сложение векторов. Для того чтобы построить сумму двух данных векторов 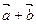 , нужно выбрать произвольную точку А и отложить от нее вектор
, нужно выбрать произвольную точку А и отложить от нее вектор 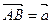 , а затем от точки В отложить вектор
, а затем от точки В отложить вектор 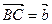 . Тогда вектор
. Тогда вектор 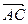 является искомой суммой:
является искомой суммой:
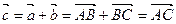
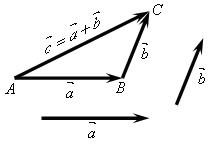
Этот способ построения называется правилом треугольника.
Сумму двух данных векторов 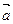 и
и 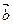 можно построить и следующим образом. Откладывая от произвольной точки О векторы
можно построить и следующим образом. Откладывая от произвольной точки О векторы 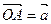 и
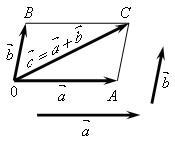
и 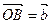 , построим параллелограмм ОАСВ. Тогда вектор
, построим параллелограмм ОАСВ. Тогда вектор 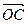 (где
(где 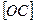 – диагональ параллелограмма) является искомой суммой:
– диагональ параллелограмма) является искомой суммой: 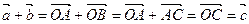 . Этот способ построения называется правилом параллелограмма:
. Этот способ построения называется правилом параллелограмма:
Вычитание векторов. Два вектора называются противоположными, если их сумма равна нулевому вектору. Вектор, противоположный вектору 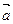 , обозначают -
, обозначают - 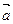 . Таким образом,
. Таким образом, 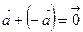 . Ненулевые противоположные векторы имеют равные длины и противоположные направления. Вектор с называется разностью векторов
. Ненулевые противоположные векторы имеют равные длины и противоположные направления. Вектор с называется разностью векторов 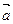 и
и 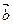 , если
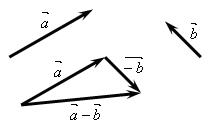
, если 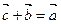 . Чтобы вычесть из вектора
. Чтобы вычесть из вектора 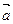 вектор
вектор 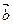 , достаточно прибавить к вектору
, достаточно прибавить к вектору 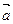 вектор, противоположный вектору
вектор, противоположный вектору 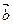 , т.е.
, т.е. 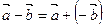
Умножение вектора на число. Произведением ненулевого вектора 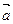 на числоm называется вектор, имеющий направление вектора
на числоm называется вектор, имеющий направление вектора 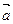 , если
, если 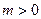 , и противоположное направление, если
, и противоположное направление, если 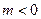 . Длина этого вектора равна произведению длины вектора
. Длина этого вектора равна произведению длины вектора 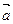 на модуль числа m.
на модуль числа m.
Произведение вектора 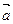 на число m обозначается m
на число m обозначается m 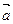 . При любых m и
. При любых m и 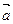 векторы m
векторы m 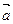 и
и 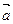 коллинеарны и
коллинеарны и 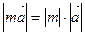 .
.
Угол между двумя векторами. Угломмеждудвумя ненулевыми векторами 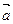 и
и 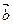 называется угол между направлениями этих векторов:
называется угол между направлениями этих векторов: 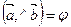 , где
, где 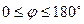 .
.
Частные случаи: 1) если 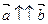 , то
, то 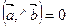 ; 2) если
; 2) если 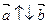 , то
, то 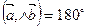 .
.
 2015-06-28
2015-06-28 339
339








