Пусть на плоскости задана пара единичных взаимно перпендикулярных векторов 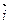 и
и 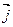 , отложенных от некоторого начала – точки О. Такую пару векторов называют прямоугольным базисом на плоскости. Совокупность начала О и прямоугольного базиса
, отложенных от некоторого начала – точки О. Такую пару векторов называют прямоугольным базисом на плоскости. Совокупность начала О и прямоугольного базиса 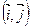 называют прямоугольнойсистемойкоординат на плоскости. Точку О называют началом координат, а векторы
называют прямоугольнойсистемойкоординат на плоскости. Точку О называют началом координат, а векторы 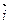 (1; 0) и
(1; 0) и 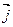 (0; 1) – координатными векторами.
(0; 1) – координатными векторами.
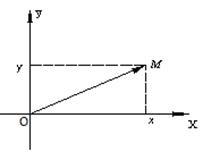
Вектор, направленный из начала координат в произвольную точку М плоскости xOy, называется радиусом–вектором точки М и обозначается 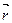 :
: 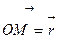
Проекции вектора 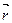 на координатные оси, т.е.
на координатные оси, т.е. 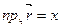 и
и 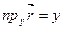 , называются координатами вектора. Координаты вектора кратко записывают так:
, называются координатами вектора. Координаты вектора кратко записывают так: 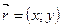 .
.
Координаты радиуса-вектора 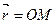 являются одновременно координатами точки M, т.е.
являются одновременно координатами точки M, т.е.
конца радиуса вектора. Если начало вектора 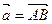 не совпадает с началом координат, то координаты вектора
не совпадает с началом координат, то координаты вектора 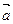 и координаты его конца различны. В этом случае проекции вектора
и координаты его конца различны. В этом случае проекции вектора 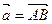 на оси координат соответственно равны
на оси координат соответственно равны 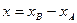 и
и 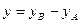 , т.е.
, т.е.

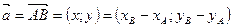 :
:
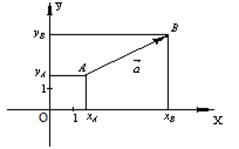
Разложение вектора по координатным осям. Разложение вектора 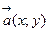 в базисе
в базисе 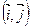 имеет вид
имеет вид 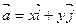 ,
,
 2015-06-28
2015-06-28 308
308








