Определение. Смешанным произведением векторов 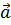 ,
, 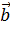 и
и 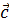 называется скалярное произведение вектора
называется скалярное произведение вектора 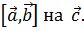
Пусть 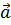 ,
, 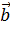 ,
, 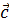 не равны нулю. Рассмотрим
не равны нулю. Рассмотрим 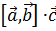 :
:
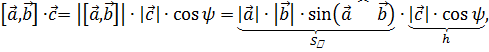
где 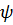 – угол между векторами – угол между векторами 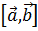 и и 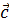 , , 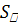 – площадь параллелограмма, построенного на векторах – площадь параллелограмма, построенного на векторах 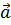 и и 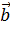 , , 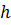 – проекция вектора – проекция вектора 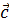 на перпендикуляр к плоскости векторов на перпендикуляр к плоскости векторов 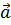 и и 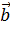 . .
| 
|
Если угол 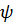 острый, то острый, то 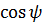 >0, и >0, и 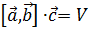 – объем параллелепипеда, построенного на векторах – объем параллелепипеда, построенного на векторах 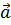 , , 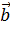 , , 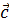 . Если угол . Если угол 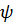 тупой, то тупой, то 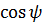 <0, и <0, и 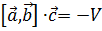 .
Значит, .
Значит, 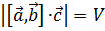 .
Таким образом, доказана .
Таким образом, доказана
| 
|
Теорема (геометрический смысл смешанного произведения трёх векторов): Если на трёх некомпланарных векторах 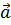 ,
, 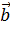 и
и 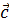 построен параллелепипед, то его объем равен модулю смешанного произведения векторов
построен параллелепипед, то его объем равен модулю смешанного произведения векторов 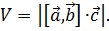
Смешанное произведение векторов в координатной форме
Пусть в репере R= 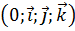 заданы векторы
заданы векторы 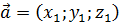 ,
, 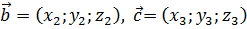 . Вычислим
. Вычислим 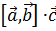 .
.
Пусть 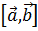 =
= 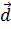 . Тогда
. Тогда 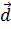 =
= 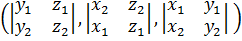 .
.
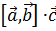 =
= 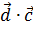 =
= 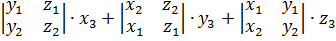 =
=
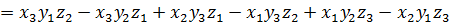 .
.
Легко проверить, что это выражение равно 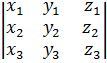 .
.
Таким образом, 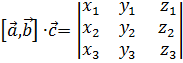 .
.
Свойства смешанного произведения векторов
Выполняются все свойства скалярного и векторного произведений векторов.
Для любых векторов 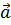 ,
, 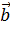 и
и 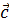 справедливо:
справедливо:
1. 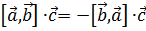 ;
;
2. 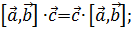
3. 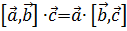 .
.
Последнее равенство можно доказать в координатной форме, например.
Часто смешанное произведение записывают 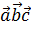 , так как из третьего свойства следует, что не важно, какую пару векторов перемножать векторно.
, так как из третьего свойства следует, что не важно, какую пару векторов перемножать векторно.
 2015-06-28
2015-06-28 251
251







