1. Докажите, что если б.ф. f является суперпозицией б.ф. g 1, …, g s, то f* является суперпозицией той же структуры функций g 1*, …, gs *.
2. Докажите, что ( Û у)* =
Û у)* =  Å у, (
Å у, ( ÷ у)* =
÷ у)* =  ¯ у, (
¯ у, ( Þ у)* =
Þ у)* = 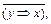
h* = h, где h ( , y, z) =
, y, z) =  y Å
y Å  z Å yz.
z Å yz.
3.10. Полином Жегалкина
Если в ЭК нет отрицаний переменных, то она называется монотонной элементарной конъюнкцией (Мон. ЭК). Например, 1,  , y,
, y,  y – все монотонные ЭК от переменных
y – все монотонные ЭК от переменных  , y; или 1, х, y, z,
, y; или 1, х, y, z,  y,
y,  z, yz,
z, yz,  yz – все Мон. ЭК от переменных
yz – все Мон. ЭК от переменных  , y, z. Сумма по модулю 2 различных монотонных элементарных конъюнкций называется полиномом Жегалкина.
, y, z. Сумма по модулю 2 различных монотонных элементарных конъюнкций называется полиномом Жегалкина.
ТЕОРЕМА. Любую булеву функцию можно представить в виде полинома Жегалкина, причем, единственным образом с точностью до коммутативности & и Å.
Доказательство. Представим б.ф. в виде СДНФ или СКНФ. С помощью тождеств 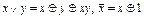 заменим все значки Ú и Ø, т.е. б.ф. представим в виде суперпозиции &, Å, 0, 1 – в виде полинома Жегалкина. Так как число всех различных полиномов Жегалкина от
заменим все значки Ú и Ø, т.е. б.ф. представим в виде суперпозиции &, Å, 0, 1 – в виде полинома Жегалкина. Так как число всех различных полиномов Жегалкина от 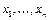 равно
равно 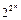 , т.е. числу всех различных n -местных б.ф., то любую б.ф. представить в виде полинома Жегалкина можно лишь единственным способом. ■
, т.е. числу всех различных n -местных б.ф., то любую б.ф. представить в виде полинома Жегалкина можно лишь единственным способом. ■
Пример. Представьте в виде полинома Жегалкина f =  Þ` y.
Þ` y.
¨ f =` x Ú` y =` x Å` y Å` x ` y = x Å 1Å y Å 1Å (x Å 1)(y Å 1) = xy Å 1.
Пример. Найдите полином Жегалкина для функции f = (11111000).
Решение. Применим метод неопределенных коэффициентов.
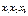 | 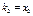 | 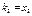 | 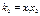 | 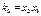 | |||||||||||||
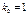 | 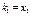 | 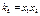 |  | ||||||||||||||
| f | |||||||||
Если 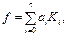 , то получим систему уравнений
, то получим систему уравнений
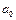 = 1
= 1 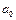 = 1
= 1
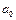 Å
Å 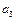 = 1
= 1 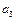 = 0
= 0
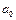 Å
Å 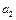 = 1
= 1 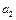 = 0
= 0
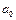 Å
Å 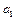 = 1
= 1 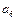 = 0
= 0
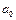 Å
Å 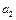 Å
Å 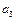 Å
Å 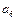 = 1
= 1 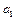 = 0
= 0
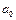 Å
Å 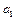 Å
Å 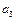 Å
Å 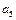 = 0
= 0 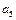 = 1
= 1
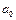 Å
Å 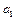 Å
Å 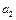 Å
Å 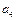 = 0
= 0 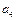 = 1
= 1
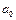 Å
Å 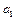 Å
Å 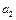 Å
Å 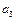 Å
Å 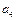 Å
Å 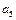 Å
Å 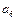 Å
Å 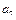 = 0
= 0 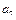 = 1
= 1
Отсюда f = K 0 Å K 4 Å K 5 Å K 7 = 1 Å  1
1  2 Å
2 Å  2
2  3 Å
3 Å  1
1  2
2  3.
3.
 2015-06-28
2015-06-28 618
618








