2015-06-28
725
Приведите к СДНФ функцию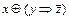 
.
Ответ: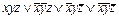 
.
3.8. Совершенная конъюнктивная нормальная форма
Конъюнкция различных элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ). Все определения и факты, приведенные для ДНФ и СДНФ, с соответствующими изменениями переносятся на КНФ и СКНФ. Таким образом, имеют место двойственные утверждения:
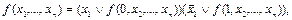
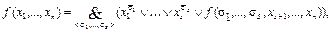
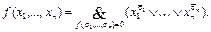
КНФ называется совершенной (СКНФ), если ранги всех ЭД, входящих в нее, равны между собой и равны числу переменных, над которыми берется форма.
ТЕОРЕМА. Для любой функции, не являющейся тождественно истинной, существует и притом единственная, эквивалентная ей СКНФ.
Доказательство.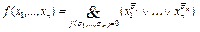 
– СКНФ. Так как числа всех различных n -местных булевых функций и СКНФ от тех же переменных совпадают, то представление булевых функций в виде СКНФ возможно единственным образом.<
Пример. Построить СКНФ для f = (10001110).
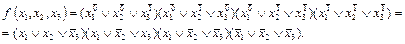
Упражнение
Приведите к СКНФ функции
1) 
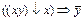; 2)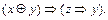 
Ответ: 1)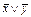 
; 2)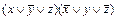 
.
3.9. Принцип двойственности
Функцию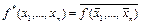 
называют двойственной функции 
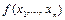. Например, 
, 
, 
, 
|
|
|
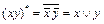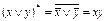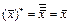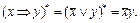
Ясно, что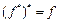 
, т.е. функции 
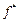и f двойственны друг другу.
ТЕОРЕМА. Если булева функция записана в виде суперпозиции &, Ú, Ø, то двойственная ей получается заменой каждой дизъюнкции на конъюнкцию, а каждой конъюнкции на дизъюнкцию.
Доказательство проведем методом полной математической индукции по числу операций над переменными. Без ограничения общности можно считать, что отрицание относится только к переменным. База индукции имеется в силу того, что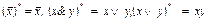 
.
Гипотеза индукции. Пусть утверждение теоремы верно для функции, получающейся с помощью s операций &, Ú, Ø.
Право перехода. Пусть дана функция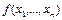 
, полученная с помощью 
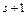операции &, Ú, Ø. Если, например, последняя операция конъюнкция, т.е. 
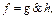то
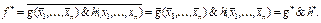
По гипотезе индукции g * и h * можно получить заменой в g и h соответственно каждой & на Ú и наоборот, т.е. f* может быть получена из f таким же образом. ■
