Дизъюнкция различных элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ). Количество ЭК, входящих в ДНФ, называется ее длиной. Сумма рангов ЭК называется сложностью ДНФ.
ТЕОРЕМА. Число всех различных ДНФ от n- переменных равно 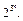
Доказательство. В ЭК переменная может входить под знаком отрицания (ситуации присваиваем код 0), может входить сама (код 1); может не входить ни сама, ни под знаком отрицания (код 2).Таким образом, каждой ЭК от n переменных ставится во взаимооднозначное соответствие размещение с повторениями из трех элементов 0, 1, 2 по n местам. Таких размещений 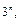 а поэтому и ЭК столько же. Любое подмножество ЭК из множества всех
а поэтому и ЭК столько же. Любое подмножество ЭК из множества всех 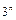 ЭК определяет ДНФ, а число всех подмножеств этого множества равно
ЭК определяет ДНФ, а число всех подмножеств этого множества равно 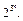 <
<
Если в ДНФ все ЭК имеют один и тот же ранг, равный числу переменных, от которых зависит ДНФ, то она называется совершенной (СДНФ).
ТЕОРЕМА о разложении булевой функции по одной переменной.
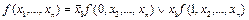
Доказательство. Проверяем, какие значения принимают функции, стоящие справа и слева, вначале на любом наборе значений переменных, начинающимся с нуля, а затем на наборе, начинающимся с единицы.<
ТЕОРЕМА о разложении булевой функции по двум переменным.
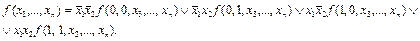 Доказательство. Применить дважды предыдущую теорему. Можно доказать также, проверяя, какие значения принимают функции, стоящие справа и слева, вначале на любом наборе значений переменных, начинающимся с двух нулей
Доказательство. Применить дважды предыдущую теорему. Можно доказать также, проверяя, какие значения принимают функции, стоящие справа и слева, вначале на любом наборе значений переменных, начинающимся с двух нулей 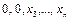 , затем на наборе вида
, затем на наборе вида 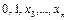 , затем на наборе вида
, затем на наборе вида 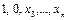 , а затем на наборе вида
, а затем на наборе вида 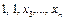 .<
.<
ТЕОРЕМА о разложении булевой функции по переменным. Любую булеву функцию 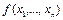 можно представить в виде
можно представить в виде
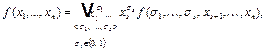 (1)
(1)
где знак сокращенной дизъюнкции берется по всем двоичным наборам 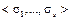
Доказательство. Можно провести индукцию по s. А можно проверить равенство непосредственно на всех наборах значений переменных. Для этого заметим, что
1) 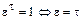 , где
, где 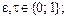
2) 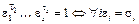 ;
;
3) 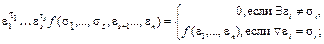
4) 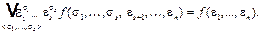 <
<
ТЕОРЕМА. Для любой функции, не являющейся тождественно ложной, существует и притом единственная СДНФ.
Доказательство. Из теоремы о разложении булевой функции по переменным при s = n следует
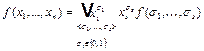 . (2)
. (2)
Но 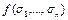 равно 0 или 1, если нулю, то соответствующее слагаемое из дизъюнкции удаляется, а если 1, то слагаемое приобретает вид
равно 0 или 1, если нулю, то соответствующее слагаемое из дизъюнкции удаляется, а если 1, то слагаемое приобретает вид 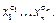 Отсюда
Отсюда 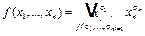 (3)
(3)
Следовательно, мы представили булеву функцию в виде СДНФ. Так как числа различных n -местных булевых функций и СДНФ совпадают, то представление булевой функции в виде СДНФ возможно лишь единственным образом.<
Следствие. Любую булеву функцию, не являющуюся тождественно ложной, можно представить в виде суперпозиции &, Ú, Ø, причем отрицание относится только к переменным.
Формула (3) позволяет по таблице истинности булевой функции строить ее СДНФ.
Пример. Привести к СДНФ функцию f = (10001110).
Таблица 3.7
|
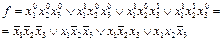
Алгоритм приведения булевой функции к ДНФ:
1) С помощью эквивалентностей 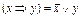 ,
,
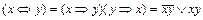 ,
, 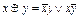 ,
, 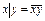 ,
, 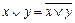 освободиться от логических связок Þ, Û, Å, ½, ¯.
освободиться от логических связок Þ, Û, Å, ½, ¯.
2) С помощью законов двойственности отнести знаки только к переменным (тесное отрицание).
3) С помощью закона дистрибутивности & относительно Ú перейти к дизъюнкции конъюнкций.
4) Воспользоваться законами идемпотентности & и Ú.
Пример. 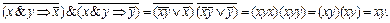
 2015-06-28
2015-06-28 2669
2669








