Жирар Дезарг (1591-1661) – французский математик, инженер и архитектор, внес существенный вклад в создание основ проективной геометрии.
Определение 1: трехвершинником на проективной плоскости P2 называется фигура, состоящая из трех точек, и лежащих на одной прямой, и трех прямых, попарно соединяющих эти точки. Указанные точки называются вершинами, а прямые – сторонами трехвершинника.

| Трехвершинник АВС Трехсторонник АВС – двойственная фигура |
Теорема 1 (прямая теорема Дезарга): если три прямые 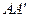 ,
, 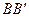 ,
, 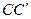 , соединяющие соответствующие вершины трехвершинников
, соединяющие соответствующие вершины трехвершинников 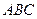 и
и 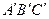 , проходят через одну точку Q, то соответствующие стороны этих трехвершинников пересекаются в трех точках, лежащих на одной прямой q.
, проходят через одну точку Q, то соответствующие стороны этих трехвершинников пересекаются в трех точках, лежащих на одной прямой q.
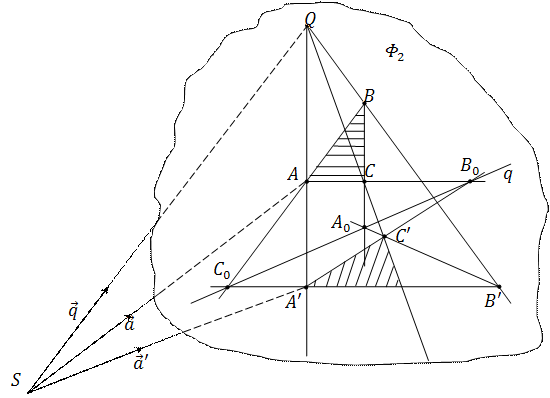
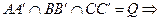
| 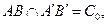 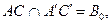
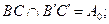 А0,В0,С0 А0,В0,С0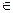 q. q.
|
- краткая запись теоремы Дезарга.
Доказательство 1 способ (методом координат):
1) Примем за координатный репер четверку точек 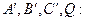
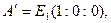
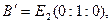
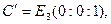
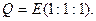
Пусть в этой проективной системе координат 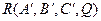
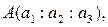
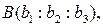
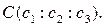 Так как точки
Так как точки  лежат на одной прямой, то определитель, составленный из их координат, равен нулю:
лежат на одной прямой, то определитель, составленный из их координат, равен нулю:


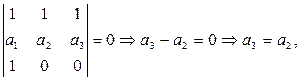
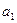 - любое число.
- любое число.
Аналогично получим, что 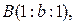
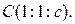
2) Найдем координаты точки 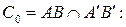
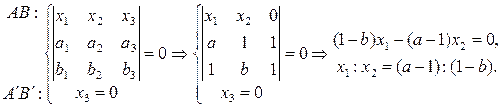
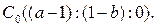
Найдем координаты точки 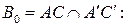
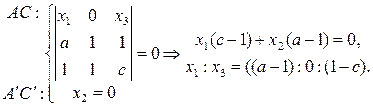
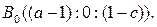
Найдем координаты точки 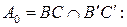
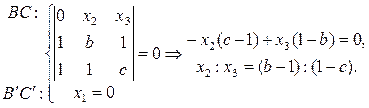
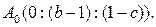
3) Точки C0, B0, A0 лежат на одной прямой, так как:
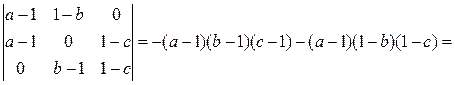
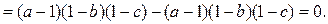
Теорема доказана.
Доказательство 2 способ:
Обозначим векторы, проходящие через точки 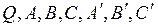 соответственно:
соответственно: 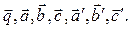 По условию прямая
По условию прямая 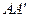 проходит через точку
проходит через точку 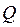 , следовательно, векторы
, следовательно, векторы 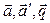 компланарны, и
компланарны, и 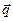 является линейной комбинацией векторов
является линейной комбинацией векторов 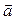 и
и 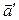 :
:
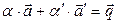 (1)
(1)
Аналогично получаем следующие равенства:
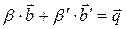 (2)
(2)
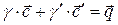 (3)
(3)
Вычтем равенство (2) из равенства (1):
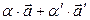 -
-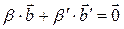
или
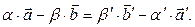
Обозначим через 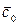 вектор, равный каждой из этих разностей:
вектор, равный каждой из этих разностей:
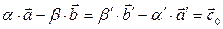 (4)
(4)
Так как 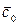 - линейная комбинация векторов
- линейная комбинация векторов 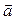 и
и 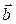 , то точка С0, порождаемая этим вектором, лежит на прямой AB:
, то точка С0, порождаемая этим вектором, лежит на прямой AB: 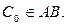
Тот же вектор 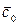 - линейная комбинация векторов
- линейная комбинация векторов 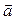 и
и 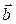 , следовательно, точка
, следовательно, точка 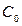 лежит также и на прямой
лежит также и на прямой 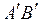 :
: 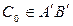 .
.
Таким образом 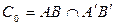 .
.
Теперь вычтем равенство (3) из равенства (1):
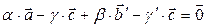
или
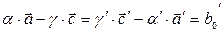 (5)
(5)
Рассуждая, как и выше, получим:
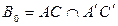 .
.
Далее, вычтем из равенства (2) равенство (3):
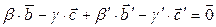
или
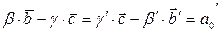 (6)
(6)
Теперь получим, что: 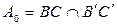 .
.
Вычтем из равенства (5) равенство (6):
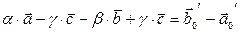 .
.
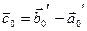 (7)
(7)
Равенство (7) показывает, что вектор 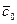 является линейной комбинацией векторов
является линейной комбинацией векторов 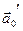 и
и 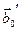 , поэтому, окончательно, точки
, поэтому, окончательно, точки 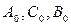 лежат на одной прямой q.
лежат на одной прямой q.
Теорема доказана.
Теорема 2 (обратная теореме Дезарга): если три точки пересечения соответствующих сторон трехвершинников АВС и 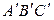 лежат на одной прямой q, то три прямые, проходящие через их соответствующие вершины, пересекаются в одной точке Q.
лежат на одной прямой q, то три прямые, проходящие через их соответствующие вершины, пересекаются в одной точке Q.
Справедливость теоремы 2 следует непосредственно по принципу двойственности из доказанной выше теоремы Дезарга.
Замечание 1: теоремы Дезарга верны и в том случае, когда данные трехвершинники лежат в разных плоскостях трехмерного проективного пространства Р3.
Определение 2: точка Q, в которой пересекаются прямые, соединяющие вершины трехвершинников, называется точкой Дезарга.
Прямая q, на которой пересекаются их соответствующие стороны, называется прямой Дезарга.
Фигура, состоящая из 10 точек и 10 прямых упоминаемых в теоремах Дезарга, называется конфигурацией Дезарга.
Замечание 2: через каждую точку конфигурации Дезарга проходят три прямые и на каждой прямой лежат три точки этой конфигурации. Любая из точек может быть принята за точку Дезарга, а любая из 10 прямых может быть принята за прямую Дезарга.
 2014-02-24
2014-02-24 6040
6040








