Замкнутые классы булевых функций.
Определение 3.2.1. Класс булевых функций 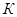 называется замкнутым, если он совпадает со своим замыканием, т.е.
называется замкнутым, если он совпадает со своим замыканием, т.е. 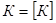 .
.
Замечание 3.2.2 Полное описание всех замкнутых классов было дано американским математиком Э. Постом. В частности, он доказал, что множество всех замкнутых классов булевых функций счетно и в каждом замкнутом классе 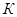 можно выделить конечную подсистему
можно выделить конечную подсистему 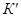 , порождающую
, порождающую 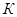 , т.е. имеющую своим замыканием класс
, т.е. имеющую своим замыканием класс 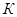 , т.е.
, т.е. 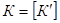 .
.
Определение 3.2.3. Булева функция 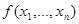 называется функцией, сохраняющей константу 0, если
называется функцией, сохраняющей константу 0, если 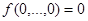 .
.
Класс всех булевых функцией, сохраняющих константу 0, обозначим 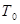 .
.
Определение 3.2.4. Булева функция 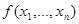 называется функцией, сохраняющей константу 1, если
называется функцией, сохраняющей константу 1, если 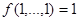 .
.
Класс всех булевых функцией, сохраняющих константу 1, обозначим 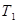 .
.
Определение 3.2.5. Булева функция 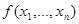 называется линейной, если
называется линейной, если 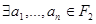 , такие,что
, такие,что 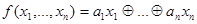 .
.
Класс всех булевых линейных функций обозначим через 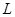 .
.
Определение 3.2.6. Булева функция 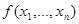 называется аффинной функцией, если
называется аффинной функцией, если 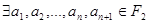 , такие, что
, такие, что 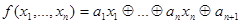 .
.
Обозначим через 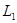 класс всех булевых аффинных функций.
класс всех булевых аффинных функций.
Определение 3.2.7. Булева функция 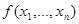 называется самодвойственной функцией, если
называется самодвойственной функцией, если 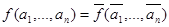
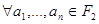 (3.2.8)
(3.2.8)
Класс всех булевых самодвойственных функций обозначим через S.
Далее определим понятие монотонной функции. Для этого нам необходимы некоторые дополнительные сведения. Изложим их. На множестве 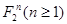 введем отношение
введем отношение 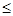 , положив для наборов
, положив для наборов 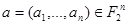 и
и 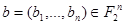 :
: 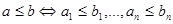 , где отношение
, где отношение 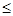 на
на 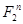 понимается как неравенство на множестве чисел {0,1}.
понимается как неравенство на множестве чисел {0,1}.
Несложно доказать, то отношение 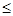 рефлексивно, транзитивно и антисимметрично, т.е. является отношением частичного порядка.
рефлексивно, транзитивно и антисимметрично, т.е. является отношением частичного порядка.
Определение 3.2.9. Булева функция 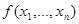 называется монотонно возрастающей, или монотонной, если для любых наборов
называется монотонно возрастающей, или монотонной, если для любых наборов 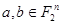 выполняется условие:
выполняется условие: 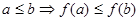
Замечание 3.2.10. Нульместные функции 0 и 1 также естественно считать монотонными.
Класс всех булевых монотонных функций обозначим через М.
Утверждение 3.2.11. Классы булевых функций 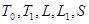 и
и 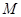 являются замкнутыми классами булевых функций.
являются замкнутыми классами булевых функций.
Для доказательства данного утверждения нам необходимо определить понятие ранга формулы 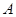 над классом
над классом 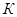 .
.
Определение 3.2.12. Число всех символов функций из 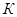 , встречающихся в формуле
, встречающихся в формуле 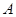 над
над 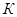 , называется рангом формулы
, называется рангом формулы 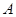 и обозначается через
и обозначается через 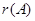 .
.
Замечание 3.2.13. Понятие ранга формулы 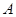 над классом
над классом 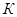 не следует путать с понятие ранга элементарной конъюнкции из определения 2.1.1.
не следует путать с понятие ранга элементарной конъюнкции из определения 2.1.1.
Доказательство утверждения 3.2.11. Замкнутость перечисленных в утверждении 3.2.11 шести классов функций доказывается по одной и той же схеме. Проделаем это для какого-нибудь одного класса, например S.
Согласно определениям замыкания (определение 3.1.1) и замкнутого класса (определение 3.2.1) нам необходимо доказать, что любая функция, представимая формулой над S, принадлежит S. Докажем это индукцией по рангу 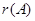 формулы А, представляющей функцию
формулы А, представляющей функцию 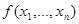 .
.
Если 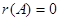 , то
, то 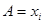 , и утверждение очевидно, так как
, и утверждение очевидно, так как 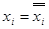 .
.
Пусть утверждение верно для всех 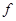 , таких что
, таких что 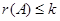 , где
, где 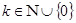 .
.
Докажем, что утверждение верно и при 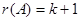 .
.
Если 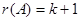 , то А имеет вид:
, то А имеет вид:  , где
, где 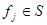 и
и 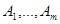 - формулы меньших рангов, чем
- формулы меньших рангов, чем 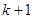 , т.е.
, т.е. 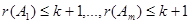 . По предположению индукции формулы
. По предположению индукции формулы 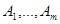 представляют булевы функции
представляют булевы функции 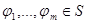 . Тогда для любых
. Тогда для любых 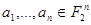 имеем:
имеем:

Следовательно, 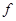 удовлетворяет условию (3.2.8), т.е
удовлетворяет условию (3.2.8), т.е 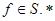
Теорема 3.3.1. Система булевых функций 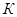 полна тогда и только тогда, когда она содержит хотя бы по одной функции каждого из следующих классов:
полна тогда и только тогда, когда она содержит хотя бы по одной функции каждого из следующих классов:
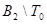 ,
, 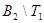 ,
, 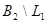 ,
, 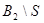 ,
, 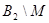 . (3.3.2)
. (3.3.2)
(без доказательства).
Пример 3.3.3. Пусть функция 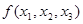 задана таблицей 3.3.4
задана таблицей 3.3.4
 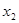 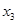 | 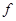 |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таблица 3.3.4
Показать, что 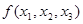 - Шефферова функция, т.е.
- Шефферова функция, т.е. 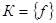 - полная система, т.е.
- полная система, т.е. 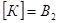 . Выразить
. Выразить 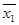 и
и 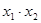 формулами над К.
формулами над К.
Решение:
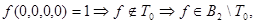
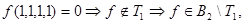
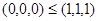 , но
, но 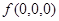 не
не 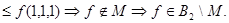
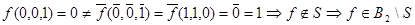 .
.
Чтобы выяснить вопрос о принадлежности 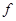 классу
классу 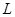 , представим
, представим 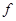 многочленом Жегалкина:
многочленом Жегалкина:
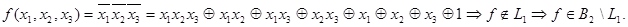 Итак, все условия теоремы 3.3.1 выполнены. Следовательно
Итак, все условия теоремы 3.3.1 выполнены. Следовательно 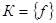 -полная система, т.е.
-полная система, т.е. 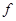 - Шефферова функция. Теперь решим вторую часть примера. Так как
- Шефферова функция. Теперь решим вторую часть примера. Так как 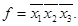 , то очевидно
, то очевидно 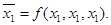 ,
, 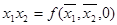 .
.
 2014-02-09
2014-02-09 2487
2487
