Совокупность множества вершин V и множества связей Е между ними называется графом и обозначается G (V, E).
На рис. 2.1 показан пример графа G (4,6), где обозначено:
V = { x 1, x 2, x 3, x 4} – множество вершин,
n = | V | = 4 – число вершин графа G (4,6),
E = { e 1, e 2, e 3, e 4, e 5, e 6} – множество ребер,

m = | E | = 6 – число ребер графа G (4,6).
E – это отображение V в V (E: V 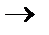 V).
V).
Рисунок 2.1
Иногда множество E называют семейством связей, так как в E могут входить направленные и ненаправленные связи, петли и все они могут быть кратными, тогда как в теории множеств одинаковые элементы представляются одним элементом.
В качестве другого примера на рис. 2.2 показано семейство графов на четырех вершинах.
Обратите внимание на общепринятые обозначения некоторых графов:
N 4 – нуль граф;
P 4 – цепь;
C 4 – цикл;
W 4 – звезда;
K 4 – полный граф, в нем каждая вершина имеет связь со всеми другими вершинами.
В общем случае эти типы графов обозначаются так:
Nn, Pn, Cn, Wn, Kn.
Обратим внимание на граф C 4. Этот граф можно представить и так, как показано на рис. 2.3. Такой граф обозначается K2,2 и называется полным двудольным графом.
В двудольном графе множество вершин V разбито на два подмножества X и Y таких, что между вершинами внутри каждого из них нет связей. Число ребер в полном двудольном графе m = n 1 n 2, где n 1 =|X|, n 2 = |Y|, n = n 1 + n 2.

Рисунок 2.2

Рисунок 2.3
Если связь имеет направление, то она называется дугой, в противном случае – ребром. (Графы с дугами и ребрами показаны на рис. 2.4.)

Рисунок 2.4
При необходимости конкретная дуга (ребро) обозначается либо собственным именем, либо парой вершин в круглых (прямых) скобках e = (v 1, v 2) – дуга e, (e = [ v 1, v2 ] – ребро e).
Граф, у которого все связи являются ребрами, называется неориентированным графом или сокращенно неорграфом (рис. 2.4, а).
Граф с дугами называется ориентированным графом или орграфом (рис. 2.4, б).
Ребро (дуга), оба конца которого связаны с одной и той же вершиной, называется петлей (рис. 2.5).
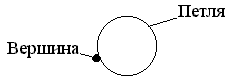
Рисунок 2.5
Если у графа существуют кратные ребра, т.е. несколько ребер, соединяющих одну и туже пару вершин, то такой граф называется мультиграфом. Если все ребра мультиграфа имеют одинаковую кратность k, то такой граф называется k –кратным или просто k –графом. На рис. 2.6 показан мультиграф G(6,20):
а, в – две вершины графа; e 1, e 2, e 3, e 4 – кратные ребра, соединяющие вершины а и в.
Граф называется псевдографом, если множество Е включает ребра, дуги, петли и все они могут быть кратными (рис. 2.7).
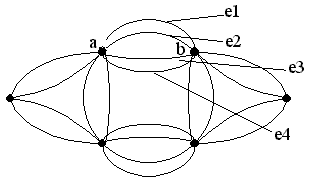
Рисунок 2.6
Две вершины называются смежными, если они соединяются некоторым ребром (дугой), и два различные ребра (дуги) смежны, если они имеют общую вершину. На рис. 2.8 у графа G (3,3) смежные вершины a и b; a и c; b и c, а также смежные дуги e 2 и e 3, смежные ребро e 1 и дуга e 2, смежные ребро e 1 и дуга e 3.
Две вершины называются смежными, если они соединяются некоторым ребром (дугой), и два различные ребра (дуги) смежны, если они имеют общую вершину. На рис. 2.8 у графа G (3,3) смежные вершины a и b; a и c; b и c, а также смежные дуги e 2 и e 3, смежные ребро e 1 и дуга e 2, смежные ребро e 1 и дуга e 3.
Вершина х инцидентна ребру (дуге) е, если она является началом или концом ребра (дуги). На рис. 2.8 вершины a и b инцидентны ребру e 1, вершины b и c инцидентны дуге e 2.
Дуга (ребро) е инцидентна вершине x, если она выходит из этой вершины или входит в нее. На рис. 2.8 дуга e 2 инцидентна вершинам b и c.
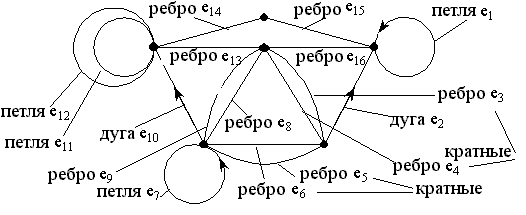
Рисунок 2.7
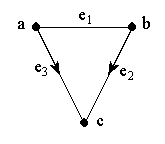
Рисунок 2.8
 2015-05-14
2015-05-14 3667
3667