Минимальные пути в нагруженных орграфах

Орграф D(V, X) называется нагруженным, если на множестве дуг X определена функция, называемая весовой, ставящая в соответствие каждой дуге некоторое действительное число l(x). Значение l(x) будем называть длиной дуги х.

Обозначим какой-либо путь в орграфе D через p, тогда l(p) – длина этого пути, равная сумме длин входящих в p дуг. Заметим, что если длины всех дуг в орграфе равны 1, то длина любого пути будет равна числу дуг в этом пути. Таким образом, можно считать ненагруженный орграф нагруженным с длинами дуг, равными 1.

Путь в нагруженном орграфе D из вершины v в вершину w (v ¹ w) называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.

Длины дуг могут быть как положительными, так и отрицательными. Рассмотрим только такие орграфы, длины дуг которых есть числа l(x) > 0.

Приведем некоторые свойства минимальных путей в нагруженных орграфах:

если для любой хÎ Х l(x) > 0, то любой минимальный путь является простой цепью;
если v₁v₂…v_k – минимальный путь, то для любых номеров i и j таких, что 1£ i£ j£ k, путь v_i v_i+1…v_j также – минимальный;
если v…uw – минимальный путь среди путей из v в w, содержащих не более k + 1 дуг, то v..u – минимальный путь среди путей из v в u, содержащих не более k дуг.

Рассмотрим теперь задачу поиска минимальных путей в орграфах.

Пусть D(V, X) – нагруженный орграф, n ³ 2. Введем величины l_i^k, где i = 1, …, n, k = 1, 2…Для каждых фиксированных i и k величина l_i^k равна длине минимального пути среди всех путей из v₁ в v_i (v₁ - начало пути), содержащего k дуг. Если таких путей нет, то l_i^k = ¥. Если произвольную вершину v считать путем из v в v нулевой длины, то величины l_i^k можно ввести для k = 0, при этом l₁⁰ = 0, l_i⁰ = ¥, i = 2,…,n.

Введем также квадратную матрицу С(D) = [c_ij], порядка n, называемую матрицей длин дуг:

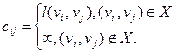
l(v_i, v_j) – длина дуги (v_i, v_j).

Для вычисления l_i^k используем формулы:

При i = 2, …,n, k ³ 0 выполняется равенство:

l_i^k+1 = min{l_j^k + c_ji},

1£ j £ n

где l_j^k – это величины всех вершин кроме i- ой, c_ji – это длины дуг из каждой j – ой вершины в i – ую, для которой вычисляется l_i^k+1.

при i = 1, k ³ 0 верно равенство:

l₁^k+1 = min{0; min{l_j^k + c_j₁}, если нет дуг отрицательной длины, то l₁^k+1 = 0.

1£ j £ n

Приведем алгоритм, позволяющий по таблице величин l_i^k, i = 1, 2,…,n, k = 0, 1, …, n – 1, определить минимальный путь в нагруженном графе D из v1 в любую достижимую вершину, причем алгоритм выделяет путь с наименьшим числом дуг.

Алгоритм носит название алгоритма Форда – Беллмана.

Шаг1. Пусть составлена таблица величин l_i^k, i = 1, 2,…,n, k = 0, 1, …, n – 1. Если l_i1^n-1 = ¥, то вершина v_i₁ не достижима из v₁. Работа алгоритма заканчивается.

Шаг2. Пусть l_i1^n-1< ¥, тогда число l_i1^n-1 выражает длину минимального пути из вершины v₁ в вершину v_i₁. Определим минимальное число дуг k₁ ³ 1, при котором выполняется равенство l_i1^k1 = l_i1^n-1. Получаем, что k₁ - минимальное число дуг в минимальном пути.

Шаг3. Последовательно определим номера вершин в этом пути i₂, …, i_k₁₊₁:

l_i2^k1-1 + c_{i2, i1} = l_i1^k1;

l_i3^k1-2 + c_{i3, i2} = l_i2^k1-1;

………………………

l_ik1+1⁰ + c_ik₁₊₁ = l_ik1¹.

Пример:

Определить минимальный путь из v1 в v6 в нагруженном орграфе D, изображенном на рисунке:

Составим матрицу длин дуг графа и рядом таблицу величин l_i^k, содержащую шесть столбцов k = 0, 1, …, 5, используя соотношения:

При i = 2, …,n, k ³ 0 выполняется равенство

l_i^k+1 = min{l_j^k + c_ji},

1£ j £ n

при i = 1, k ³ 0 верно равенство

l₁^k+1 = min{0; min{l_j^k + c_j₁},

1£ j £ n

V₁

V₂

V₃

V₄

V₅

V₆

l_i⁰

l_i¹

l_i²

l_i³

l_i⁴

l_i⁵

V₁

V₂

V₃

V₄

V₅

V₆

Первый столбец значений l_i^k: l₁⁰= 0 (начало пути), остальные - ¥. Вся первая строка содержит нули, т.к. это начало пути и 0 – наименьшая длина из v₁ в v₁.

Второй столбец: l_i¹ – это длины дуг, соединяющих v₁ с другими вершинами и, начиная со второй вершины, заносим значения из первой строки матрицы длин дуг.

Третий столбец: l₂² = min{0+¥, 5+2, 5+2, 2+¥, 12+¥}= 7;

l₃² = min {0+5, ¥+¥, 5+¥, 2+1, 12+¥}=3;

l₄² = min{0+5, ¥+¥, 5+¥, 2+2,12+¥}= 4;

l₅² = min{0+2, ¥+¥,5+¥,5+¥,12+¥} = 2;

l₆² = min{0+12, ¥+2,5+¥,5+¥,2+¥} = 12.

Четвертый столбец:

l₂³ = min{0+¥, 3+2, 4+2, 2+¥, 12+¥}= 5;

l₃³ = min {0+5, 7+¥, 4+¥, 2+1, 12+¥}=3;

l₄³ = min{0+5, 7+¥, 3+¥, 2+2,12+¥}= 4;

l₅³ = min{0+2, 7+¥,3+¥,4+¥,12+¥} = 2;

l₆³ = min{0+12, 7+2,3+¥,4+¥,2+¥} = 9.

Пятый столбец: