Эйлеровой характеристикой связного плоского графа G называется число 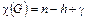 ,
,
где n – число вершин графа G;
h – число его рёбер;
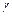 – число областей, на которые G делит плоскость, включая и бесконечную область. Например, для графа, изображённого на рис. 5.6, имеем
– число областей, на которые G делит плоскость, включая и бесконечную область. Например, для графа, изображённого на рис. 5.6, имеем 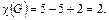
 Пусть даны два графа G и
Пусть даны два графа G и 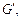 пусть
пусть 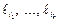 – части, на которые дуги графа
– части, на которые дуги графа 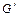 делят дугу
делят дугу 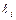 графа G,
графа G, 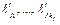 определены аналогично. Граф G с рёбрами
определены аналогично. Граф G с рёбрами 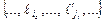 называется наложением графов G и
называется наложением графов G и 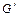 .
.
Лемма 1. Пусть связный плоский граф 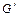 получен из связного плоского графа G наложением ребра
получен из связного плоского графа G наложением ребра 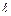 с несовпадающими концами. Тогда
с несовпадающими концами. Тогда 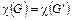 .
.
Доказательство. Очевидно, что пересечение графа G и ребра 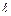 не пусто, иначе
не пусто, иначе 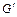 не мог бы быть связным. Пусть a, b – концы отрезка
не мог бы быть связным. Пусть a, b – концы отрезка 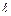 , а
, а 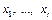 – точки пересечения
– точки пересечения 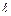 и G.
и G.
Случай 1. Ни одна из точек 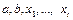 не совпадает ни с одной из вершин графа G. Тогда число вершин в графе
не совпадает ни с одной из вершин графа G. Тогда число вершин в графе 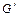 равно
равно 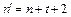 . Если на граф G наложить отрезок
. Если на граф G наложить отрезок 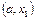 , то число рёбер увеличится на 2, а число областей не изменится (рис. 5.7).
, то число рёбер увеличится на 2, а число областей не изменится (рис. 5.7).
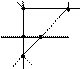
При последовательном наложении отрезков 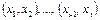 число рёбер увеличивается с каждым шагом на 2, а число областей на 1 (рис. 5.8). При добавлении же отрезка
число рёбер увеличивается с каждым шагом на 2, а число областей на 1 (рис. 5.8). При добавлении же отрезка 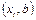 число рёбер увеличивается на 1, а число областей не изменяется (рис. 5.9), т.е. имеем
число рёбер увеличивается на 1, а число областей не изменяется (рис. 5.9), т.е. имеем 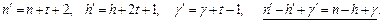
 | |||||
 | |||||
 | |||||
|
|
|
|
|
а
Рис. 5.7 Рис. 5.8 Рис. 5.9
Способ 2. Пусть некоторые из точек 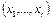 являются вершинами графа G. И пусть число таких точек k
являются вершинами графа G. И пусть число таких точек k 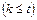 . Тогда
. Тогда
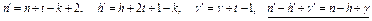
Случай 3. Пусть точка а принадлежит графу G. Добавим к отрезку 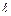 кусок так, чтобы он пересекался с G только в точке а (рис. 5.10). При этом эйлерова характеристика не изменилась и задача свелась к уже разобранному случаю. Остальные случаи очевидны.
кусок так, чтобы он пересекался с G только в точке а (рис. 5.10). При этом эйлерова характеристика не изменилась и задача свелась к уже разобранному случаю. Остальные случаи очевидны.
 Лемма 2. Пусть связный граф
Лемма 2. Пусть связный граф 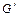 получен наложением графа
получен наложением графа 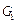 на граф G. Тогда
на граф G. Тогда 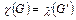 .
.
Доказательство. Проведём индукцию по числу рёбер h графа 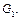 Лемма 1 даёт базис индукции. Предположим, что утверждение верно для графа
Лемма 1 даёт базис индукции. Предположим, что утверждение верно для графа 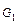 с числом рёбер h. Рассмотрим теперь граф с h + 1 ребром.
с числом рёбер h. Рассмотрим теперь граф с h + 1 ребром.
Случай 1. В графе 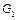 найдутся два ребра, которые пересекаются с рёбрами графа G. Удаляя ребро графа
найдутся два ребра, которые пересекаются с рёбрами графа G. Удаляя ребро графа 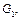 не являющееся перешейком, получим граф
не являющееся перешейком, получим граф 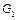 с h рёбрами такой, что наложение
с h рёбрами такой, что наложение 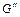 графа
графа 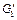 на граф G связно. По индукционному предположению
на граф G связно. По индукционному предположению 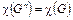 . Добавляя удалённое ребро по лемме 1, получим
. Добавляя удалённое ребро по лемме 1, получим 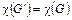 .
.
Случай 2. Граф 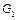 пересекается с графом G по одному ребру
пересекается с графом G по одному ребру 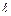 . Если граф
. Если граф 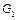 не дерево, то в нём есть цикл. Удаляя ребро этого цикла, не совпадающее с
не дерево, то в нём есть цикл. Удаляя ребро этого цикла, не совпадающее с 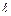 и аналогично случаю 1, получим
и аналогично случаю 1, получим 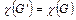 . Если же
. Если же 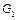 – дерево, то в нем имеются по крайней мере два концевых ребра (тупика). Удаляя не совпадающий с
– дерево, то в нем имеются по крайней мере два концевых ребра (тупика). Удаляя не совпадающий с 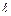 тупик, с помощью тех же рассуждений получим, что эйлеровы характеристики графов G и
тупик, с помощью тех же рассуждений получим, что эйлеровы характеристики графов G и 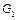 совпадают.
совпадают.
ТЕОРЕМА. Для любого плоского связного графа G имеем 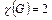 .
.
Доказательство. Рассмотрим два плоских непересекающихся связных графа G 1 и G 2. Пусть 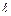 – дуга, одна вершина которой принадлежит
– дуга, одна вершина которой принадлежит 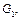 а другая G 2. Пусть
а другая G 2. Пусть 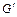 – наложение
– наложение 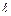 на
на 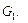 По лемме 2
По лемме 2 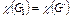 , поскольку граф
, поскольку граф 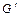 связан. Кроме того, наложение
связан. Кроме того, наложение 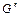 графа
графа 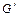 на граф G 2 также связно, а поэтому
на граф G 2 также связно, а поэтому 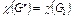 . Аналогично получим
. Аналогично получим  . Из произвольности графов и получаем, что любые два плоских связных графа имеют одну и ту же эйлерову характеристику. Поэтому достаточно подсчитать её для простейшего плоского связного графа.<
. Из произвольности графов и получаем, что любые два плоских связных графа имеют одну и ту же эйлерову характеристику. Поэтому достаточно подсчитать её для простейшего плоского связного графа.<
Замечание. Условие связности графа существенно для доказательства теоремы. Например, для несвязного графа 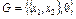 имеем
имеем 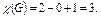
 2015-06-28
2015-06-28 802
802








