Задача о кенигсбергских мостах. Постановка и решение этой задачи Эйлером знаменует начало разработки теории графов. Расположение мостов через реку Прегель в г. Кенигсберге в его время приведено на рис. 5.13.












































































Требуется пройти каждый мост по одному разу и вернуться в исходную часть города. Можно построить граф задачи, в которой каждой части города соответствует вершина, а каждому мосту – ребро, инцидентное вершинам, относящимся к соединяемым им частям (рис. 5.14). Обходу мостов соответствует маршрут графа, который по условию должен быть простым циклом. Эйлеровой цепью графа называется маршрут, включающий все рёбра графа и через каждое ребро проходящей по одному разу. Замкнутая эйлерова цепь – эйлеров цикл. Эйлерову цепь и эйлеров цикл называют эйлеровыми графами.
ТЕОРЕМА. Граф имеет эйлеров цикл 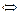 а) связен, б) все его вершины имеют положительные чётные степени.
а) связен, б) все его вершины имеют положительные чётные степени.
Доказательство. Необходимость очевидна.
Докажем вначале, что в графе 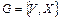 , все вершины которого имеют чётную степень, для любого ребра x найдётся цикл, содержащий x. Пусть a 0, a 1 – концы ребра x. Так как степень вершины a 1 чётна, то найдётся другое ребро x 2, отличное от x, инцидентное a 1. Пусть a 2 – вторая концевая точка ребра x 2. Маршрут
, все вершины которого имеют чётную степень, для любого ребра x найдётся цикл, содержащий x. Пусть a 0, a 1 – концы ребра x. Так как степень вершины a 1 чётна, то найдётся другое ребро x 2, отличное от x, инцидентное a 1. Пусть a 2 – вторая концевая точка ребра x 2. Маршрут 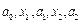 простой. Продолжая таким образом
простой. Продолжая таким образом 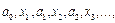 получим последовательность простых маршрутов увеличивающейся длины. В силу конечности графа через некоторое время продлить маршрут будет невозможно. Это значит, что маршрут заканчивается в вершине a 0.
получим последовательность простых маршрутов увеличивающейся длины. В силу конечности графа через некоторое время продлить маршрут будет невозможно. Это значит, что маршрут заканчивается в вершине a 0.
Рассмотрим в графе G замкнутый простой маршрут 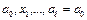 , содержащий наибольшее число рёбер. Покажем, что в графе нет вершин, не лежащих на этом маршруте. Предположим, что некоторая вершина b не лежит на нём. Так как граф связан, то существуют цепи между b и каждой из всех вершин
, содержащий наибольшее число рёбер. Покажем, что в графе нет вершин, не лежащих на этом маршруте. Предположим, что некоторая вершина b не лежит на нём. Так как граф связан, то существуют цепи между b и каждой из всех вершин 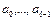 максимального маршрута. Рассмотрим самую короткую цепь
максимального маршрута. Рассмотрим самую короткую цепь 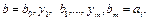 Вершины
Вершины 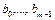 не могут совпадать с вершинами
не могут совпадать с вершинами 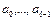 , в противном случае можно было бы выбрать цепь длины < m. Следовательно, ребро ym не входит в выбранный путь.
, в противном случае можно было бы выбрать цепь длины < m. Следовательно, ребро ym не входит в выбранный путь.
Из множества рёбер графа удалим 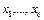 и полученное множество рёбер обозначим через
и полученное множество рёбер обозначим через 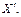 В графе
В графе 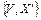 все вершины имеют чётную степень, т.е. в нём существует простой замкнутый маршрут, включающий ребро ym. Пусть это будет маршрут
все вершины имеют чётную степень, т.е. в нём существует простой замкнутый маршрут, включающий ребро ym. Пусть это будет маршрут 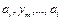 .
.
Если в исходный маршрут вместо ai подставить этот маршрут, то получим маршрут длины > 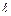 . Это противоречит тому, что
. Это противоречит тому, что 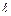 – максимальная длина простого замкнутого маршрута в графе. Итак, простой замкнутый маршрут максимальной длины проходит через все вершины графа.
– максимальная длина простого замкнутого маршрута в графе. Итак, простой замкнутый маршрут максимальной длины проходит через все вершины графа.
Предположим, что он содержит не все рёбра графа. Тогда в графе найдётся ребро y, инцидентное одной из вершин ai и не входящее в максимальный маршрут. Повторив рассуждения, проведённые для ym, получим противоречие.<
Следствие. Граф имеет открытую эйлерову цепь 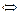 а) связен, б) содержит ровно две вершины нечётной степени.
а) связен, б) содержит ровно две вершины нечётной степени.
Необходимость очевидна.
 Пусть a, b – две вершины нечётной степени. Соединим их ещё одним ребром x. После этого все вершины графа приобретут чётную степень, т.е. в нём существует замкнутая эйлерова цепь. Осталось удалить из неё ребро x. <
Пусть a, b – две вершины нечётной степени. Соединим их ещё одним ребром x. После этого все вершины графа приобретут чётную степень, т.е. в нём существует замкнутая эйлерова цепь. Осталось удалить из неё ребро x. <
Гамильтоновой цепью графа называется цепь, которая проходит через все вершины графа и через каждую проходит по одному разу. Гамильтоновым циклом называется замкнутая гамильтонова цепь.
ТЕОРЕМА. Если число вершин графа n > 3 и степени всех вершин больше, чем n /2, то граф гамильтонов.<











































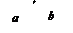
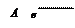

















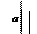

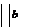
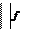





















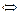 а) связен, б) все его вершины имеют положительные чётные степени.
а) связен, б) все его вершины имеют положительные чётные степени.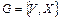 , все вершины которого имеют чётную степень, для любого ребра x найдётся цикл, содержащий x. Пусть a 0, a 1 – концы ребра x. Так как степень вершины a 1 чётна, то найдётся другое ребро x 2, отличное от x, инцидентное a 1. Пусть a 2 – вторая концевая точка ребра x 2. Маршрут
, все вершины которого имеют чётную степень, для любого ребра x найдётся цикл, содержащий x. Пусть a 0, a 1 – концы ребра x. Так как степень вершины a 1 чётна, то найдётся другое ребро x 2, отличное от x, инцидентное a 1. Пусть a 2 – вторая концевая точка ребра x 2. Маршрут 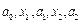 простой. Продолжая таким образом
простой. Продолжая таким образом 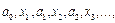 получим последовательность простых маршрутов увеличивающейся длины. В силу конечности графа через некоторое время продлить маршрут будет невозможно. Это значит, что маршрут заканчивается в вершине a 0.
получим последовательность простых маршрутов увеличивающейся длины. В силу конечности графа через некоторое время продлить маршрут будет невозможно. Это значит, что маршрут заканчивается в вершине a 0.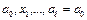 , содержащий наибольшее число рёбер. Покажем, что в графе нет вершин, не лежащих на этом маршруте. Предположим, что некоторая вершина b не лежит на нём. Так как граф связан, то существуют цепи между b и каждой из всех вершин
, содержащий наибольшее число рёбер. Покажем, что в графе нет вершин, не лежащих на этом маршруте. Предположим, что некоторая вершина b не лежит на нём. Так как граф связан, то существуют цепи между b и каждой из всех вершин 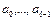 максимального маршрута. Рассмотрим самую короткую цепь
максимального маршрута. Рассмотрим самую короткую цепь 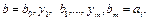 Вершины
Вершины 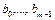 не могут совпадать с вершинами
не могут совпадать с вершинами 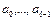 , в противном случае можно было бы выбрать цепь длины < m. Следовательно, ребро ym не входит в выбранный путь.
, в противном случае можно было бы выбрать цепь длины < m. Следовательно, ребро ym не входит в выбранный путь.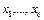 и полученное множество рёбер обозначим через
и полученное множество рёбер обозначим через 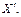 В графе
В графе 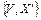 все вершины имеют чётную степень, т.е. в нём существует простой замкнутый маршрут, включающий ребро ym. Пусть это будет маршрут
все вершины имеют чётную степень, т.е. в нём существует простой замкнутый маршрут, включающий ребро ym. Пусть это будет маршрут 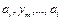 .
.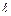 . Это противоречит тому, что
. Это противоречит тому, что 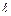 – максимальная длина простого замкнутого маршрута в графе. Итак, простой замкнутый маршрут максимальной длины проходит через все вершины графа.
– максимальная длина простого замкнутого маршрута в графе. Итак, простой замкнутый маршрут максимальной длины проходит через все вершины графа. а) связен, б) содержит ровно две вершины нечётной степени.
а) связен, б) содержит ровно две вершины нечётной степени. Пусть a, b – две вершины нечётной степени. Соединим их ещё одним ребром x. После этого все вершины графа приобретут чётную степень, т.е. в нём существует замкнутая эйлерова цепь. Осталось удалить из неё ребро x. <
Пусть a, b – две вершины нечётной степени. Соединим их ещё одним ребром x. После этого все вершины графа приобретут чётную степень, т.е. в нём существует замкнутая эйлерова цепь. Осталось удалить из неё ребро x. < 2015-06-28
2015-06-28 716
716








