Самоприменимости

Проблема самоприменимости заключается в построении алгоритма, позволяющего выяснить, применима ли МТ к своему номеру.

ТЕОРЕМА. Проблема самоприменимости алгоритмически неразрешима.

Доказательство. Допустим, что существует алгоритм, позволяющий выяснить, применима ли МТ к своему номеру. Обозничим через МС машину Тьюринга, разрешающую этот алгоритм, и пусть МС печатает 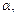если машина 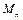применима к 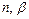в противном случае. Пусть 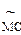зацикливается, если МС выдает 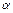и совпадает с МС в остальных случаях, и пусть æ – номер 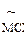. Допустим 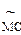самоприменима. Тогда МС(æ) = 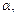а следовательно, 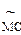при работе над æ зацикливается. Если же допустим, что 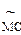не самоприменима, то МС (æ) = 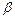, т.е. 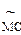применима к своему номеру, т.е. самоприменима. Противоречие. ■