Поставим булеву функцию 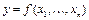 во взаимнооднозначное соответствие множеств
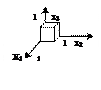
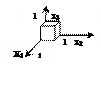
во взаимнооднозначное соответствие множеств 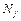 всех двоичных наборов, на которых функция принимает значение 1. Множество всех двоичных наборов, на которых элементарная конъюнкция ранга r принимает значение 1, называется интервалом ранга r. В качестве примера приведем все интервалы для ЭК (
всех двоичных наборов, на которых функция принимает значение 1. Множество всех двоичных наборов, на которых элементарная конъюнкция ранга r принимает значение 1, называется интервалом ранга r. В качестве примера приведем все интервалы для ЭК (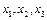 ) (табл. 8.1).
) (табл. 8.1).
Таблица 8.1
| ЭК | Интервалы | ЭК | Интервалы |
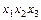
|    111 111
| 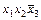
| 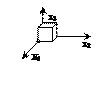  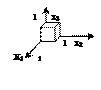 110 110
|
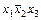
| 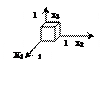  101 101
| 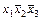
| |
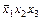
|  011 011
| 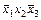
| 010  
|
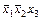
|  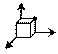 001 001
| 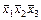
|  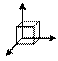 000 000
|
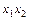
| 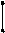 111 111
| 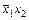
| 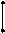 011 011
|
Продолжение табл. 8.1
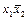
|  101 101
| 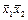
|  001 001
| ||||||
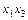
|
101 111 | 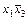
|
100 110 | ||||||
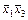
|
000 010 | 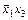
|
001 011 | ||||||
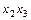
|
 111 111
| 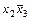
|
010 110 | ||||||
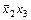
|
001 101 | 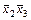
|
000 100 | ||||||
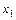
|  101 111
100 110 101 111
100 110
| 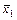
|  001 011
000 010 001 011
000 010
| ||||||
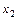
|  111 011 111 011
| 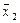
|  001 101 001 101
| ||||||
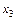
| 001 101
 011 111
011 111
| 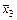
|  000 100
010 110 000 100
010 110
| ||||||
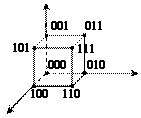
|
ТЕОРЕМА. 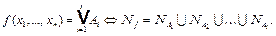
 2015-06-28
2015-06-28 309
309