Глава 8. Минимизация булевых функций

Сумма всех рангов элементарных дизъюнкций, входящих в ДНФ, называется сложностью ДНФ. ДНФ для булевой функции называется минимальной, если она реализует эту функцию и имеет минимальную сложность среди всех ДНФ, реализующих эту функцию. Задача – построить минимальную ДНФ для булевой функции. Как известно, число всех различных булевых функций от 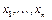равно 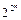, а число ДНФ от этих же переменных равно 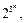т.е. “в среднем” на булевых функций приходится 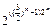, реализующих её ДНФ. Среди них мы и должны выбрать минимальную ДНФ.