Рассматриваются частичные числовые функции 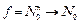 . Функция f называется всюду определенной, если она определена на всем множестве
. Функция f называется всюду определенной, если она определена на всем множестве 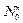 . Следующие всюду определенные функции называются простейшими:
. Следующие всюду определенные функции называются простейшими: 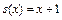 – функция следования,
– функция следования, 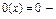 нулевая функция,
нулевая функция, 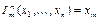 – селекторная функция, т.е. функция выбора аргумента. Функция
– селекторная функция, т.е. функция выбора аргумента. Функция 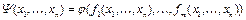 получена из функций
получена из функций 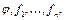 с помощью оператора суперпозиции. Функция
с помощью оператора суперпозиции. Функция 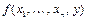 получается из функций
получается из функций 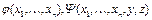 с помощью оператора примитивной рекурсии, если она может быть задана схемой:
с помощью оператора примитивной рекурсии, если она может быть задана схемой:
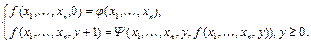
Её обозначение 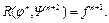 При n = 0 схема примитивной рекурсии имеет вид:
При n = 0 схема примитивной рекурсии имеет вид: 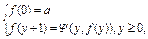
где a – постоянная одноместная функция, равная a. Тогда имеем
| y | … | ||||
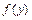 | a | 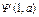 | 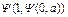 | 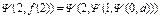 | … |
Будем говорить, что функция 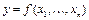 получается из функции
получается из функции 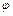 с помощью оператора минимизации по переменной x (
с помощью оператора минимизации по переменной x (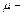 оператор), если
оператор), если 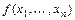 определено и равно y
определено и равно y 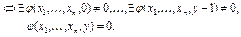
Обозначение: 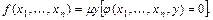
Функция f называется примитивно рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции С и примитивной рекурсии R. Множество всех примитивно рекурсивных функций обозначается как 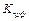 . Функция называется частично рекурсивной, если она может быть получена из простейщих функций с помощью конечного числа применений операторов С, R,
. Функция называется частично рекурсивной, если она может быть получена из простейщих функций с помощью конечного числа применений операторов С, R, 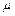 . Это множество обозначается
. Это множество обозначается 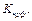 Функция называется общерекурсивной, если она частично рекурсивна и всюду определена
Функция называется общерекурсивной, если она частично рекурсивна и всюду определена 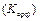 . Ясно, что
. Ясно, что 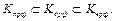
ТЕОРЕМА. 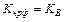 – класс всех функций, вычислимых по Тьюрингу.
– класс всех функций, вычислимых по Тьюрингу.
Доказательство. Приведем машины Тьюринга для простейших функций:
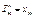 | 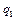 | … | 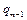 | 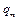 | 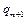 | … | 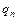 | 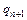 | 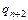 | 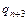 | |||||||
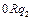 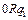 | … … | 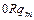 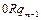 | 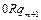 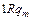 | 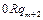 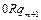 | … … | 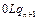 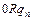 | 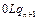 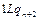 | 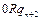 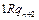 | |||||||||
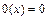 | 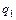 | 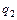 | 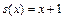 | 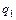 | 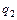 | ||||||||||||
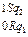 | 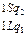 | ||||||||||||||||
Остальные выкладки доказательства опустим.
 2015-06-28
2015-06-28 1161
1161
