К линейным операциям над векторами относятся операции умножения вектора на число и сложение векторов.
Определение 5. Под произведением вектора  на число
на число 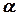 понимается вектор
понимается вектор 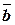 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 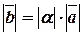 ;
;
2) вектор 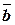 коллинеарен вектору
коллинеарен вектору  (
(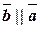 );
);
3) векторы 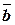 и
и  направлены одинаково, если
направлены одинаково, если 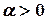 и противоположно, если
и противоположно, если 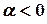 .
.
Произведение вектора  на число
на число 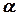 обозначается
обозначается 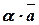 .
.
Замечание 1. Пусть 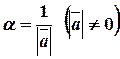 , рассмотрим вектор
, рассмотрим вектор 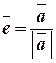 , тогда
, тогда 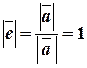 . Векторы
. Векторы 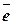 и
и  коллинеарные и одинаково направлены, тогда
коллинеарные и одинаково направлены, тогда 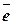 - единичный вектор, сонаправленный с
- единичный вектор, сонаправленный с  . Вектор
. Вектор 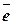 - орт вектора
- орт вектора  , и обозначается
, и обозначается  0, т.е.
0, т.е. 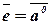 и
и 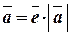 или
или 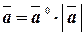 .
.
Замечание 2. Пусть дан вектор 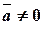 . Для любого коллинеарного ему вектора
. Для любого коллинеарного ему вектора 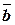 существует и притом одно число
существует и притом одно число 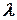 , удовлетворяющее равенству
, удовлетворяющее равенству 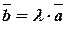 . Тогда
. Тогда 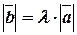 и
и 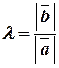 , если
, если 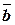 и
и  одинаково направлены и
одинаково направлены и 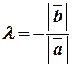 , если они противоположно направлены.
, если они противоположно направлены.
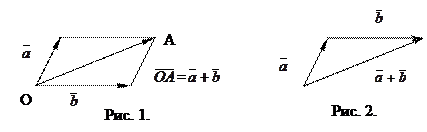 Определение 6. Суммой двух векторов
Определение 6. Суммой двух векторов  и
и 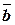 , приведенных к общему началу, является диагональ параллелограмма (
, приведенных к общему началу, является диагональ параллелограмма (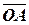 см. рис. 1), построенного на этих векторах как на сторонах (правило параллелограмма). Правило треугольника:
см. рис. 1), построенного на этих векторах как на сторонах (правило параллелограмма). Правило треугольника:
начало следующего вектора поместить в конец предыдущего и вектор, соединяющий начало первого с концом последнего есть вектор суммы (см. рис. 2).
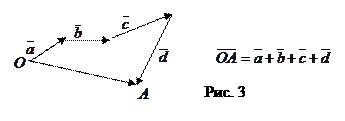 Чтобы сложить несколько векторов, достаточно начало каждого последующего вектора совместить с концом предыдущего, тогда замыкающий вектор, идущий из начала первого в конец последнего, будет вектором суммы (правило многоугольника см. рис. 3).
Чтобы сложить несколько векторов, достаточно начало каждого последующего вектора совместить с концом предыдущего, тогда замыкающий вектор, идущий из начала первого в конец последнего, будет вектором суммы (правило многоугольника см. рис. 3).
Если точка 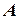 совпадает с точкой
совпадает с точкой 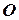 , то сумма векторов равна нулю.
, то сумма векторов равна нулю.
Определение 7. Вектором, противоположным к данному вектору  , называется вектор
, называется вектор 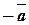 , модуль которого равен модулю вектора
, модуль которого равен модулю вектора  , а направление противоположно (см. рис. 4).
, а направление противоположно (см. рис. 4).
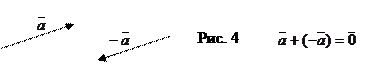 |
Определение 8. Под разностью двух векторов  и
и 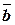 понимается такой третий вектор
понимается такой третий вектор 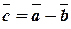 , который при сложении с вычитаемым вектором
, который при сложении с вычитаемым вектором 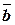 дает уменьшаемый вектор
дает уменьшаемый вектор  .
.
Правило построения разности векторов  и
и 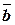 :
:
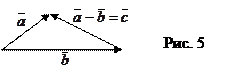 |
Приводим векторы
 и
и 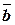 к общему началу, и соединяем концы векторов
к общему началу, и соединяем концы векторов  и
и 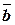 . Вектор разности направлен из конца вычитаемого вектора (
. Вектор разности направлен из конца вычитаемого вектора (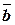 ) в конец уменьшаемого вектора (
) в конец уменьшаемого вектора ( см. рис. 5).
см. рис. 5). 2015-06-28
2015-06-28 778
778








