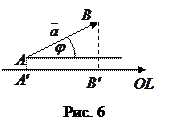 Пусть дан вектор
Пусть дан вектор  и ось
и ось  ,
,  - угол между вектором
- угол между вектором  и положительным направлением оси
и положительным направлением оси  .
. 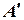 и
и 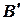 - основания перпендикуляров, опущенных из точек
- основания перпендикуляров, опущенных из точек 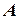 и
и 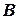 соответственно (см. рис. 6).
соответственно (см. рис. 6).
Определение 15.Проекцией вектора на ось называется длина отрезка оси 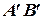 , взятая со знаком плюс, если вектор
, взятая со знаком плюс, если вектор  образует острый угол с направлением оси, и со знаком минус в противоположном случае.
образует острый угол с направлением оси, и со знаком минус в противоположном случае.
Теорема 2. Проекция вектора  на ось
на ось 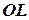 равна произведению длины вектора на косинус угла между вектором и осью:
равна произведению длины вектора на косинус угла между вектором и осью: 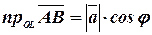 .
.
Следствие. При умножении вектора  на некоторое число
на некоторое число 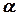 его проекция умножается на это же число:
его проекция умножается на это же число: 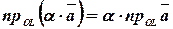 .
.
Теорема 3 (о проекции суммы). Проекция суммы некоторого числа векторов на ось 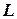 равна сумме проекций слагаемых векторов:
равна сумме проекций слагаемых векторов: 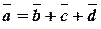 ,
, 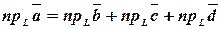 .
.
Декартова система координат.
Ортонормированный базис образуют взаимно перпендикулярные векторы 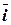 ,
, 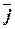 ,
, 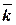 единичной длины, т.е.
единичной длины, т.е.
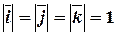 и
и 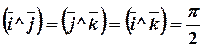 .
.
Точка  - начало координат
- начало координат  . Прямые, проходящие через начало координат в направлении векторов
. Прямые, проходящие через начало координат в направлении векторов  ,
, 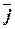 ,
, 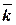 , называются осями координат. Векторы
, называются осями координат. Векторы 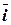 ,
, 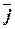 ,
, 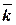 соответствуют положительному направлению осей координат:
соответствуют положительному направлению осей координат: 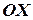 ,
, 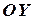 ,
, 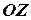 - оси абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями
- оси абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями 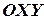 ,
, 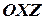 ,
, 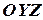 (см. рис. 7).
(см. рис. 7).
Определение 16. Прямоугольной системой координат называется совокупность точки (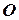 ) и ортонормированного базиса.
) и ортонормированного базиса.
Определение 17. Радиус-вектором произвольной точки 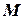 по отношению к точке
по отношению к точке 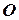 , называется вектор
, называется вектор 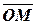 . Точке
. Точке 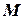 можно сопоставить упорядоченную тройку чисел (
можно сопоставить упорядоченную тройку чисел (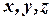 ) - компоненты ее радиус-вектора:
) - компоненты ее радиус-вектора: 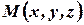 и
и 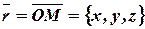 (см. рис. 8).
(см. рис. 8).
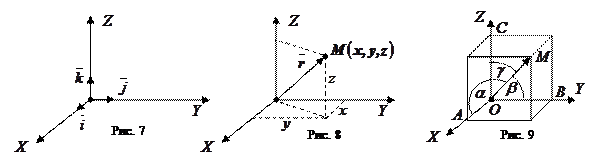 |
Определение 18. Компоненты радиус-вектора точки
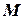 по отношению к началу координат называют координатами точки
по отношению к началу координат называют координатами точки 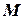 в рассматриваемой системе координат.
в рассматриваемой системе координат. Координаты вектора совпадают с проекцией вектора на соответствующие оси координат (рис.8):
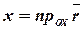 ,
, 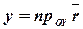 ,
, 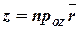 ,
, 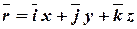 ,
, 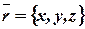
Согласно рис. 9 имеем: 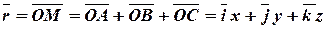 ,
, 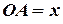 ,
, 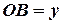 ,
, 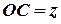 ,
,
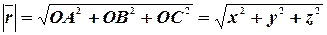 .
.
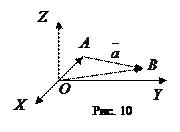 |
Пусть вектор
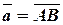 задан координатами крайних точек,
задан координатами крайних точек, 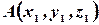 и
и 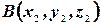 (рис. 10).
(рис. 10).
Тогда
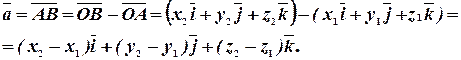
Следовательно, чтобы определить координаты вектора по координатам крайних точек, надо из координат конца вычесть соответствующие координаты начала: 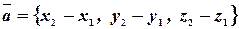 .
.
Определение 19. Пусть 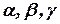 - углы между вектором
- углы между вектором  и соответственно ортами
и соответственно ортами 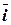 ,
, 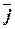 ,
, 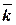 (рис. 9), тогда направляющие косинусы вектора
(рис. 9), тогда направляющие косинусы вектора 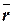 определяются по правилу:
определяются по правилу:
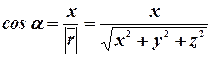 ,
,
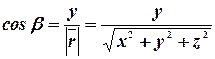 ,
,
 ,
,
Следовательно, сумма квадратов направляющих косинусов равна 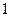 :
: 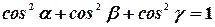 .
.
Пример 1. Даны точки 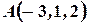 ,
, 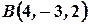 ,
, 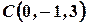 ,
, 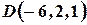 .
.
Найти координаты и длину вектора 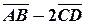 .
.
Решение. Найдем координаты векторов 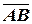 и
и 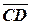 :
:
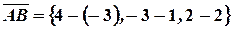 ,
, 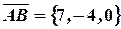 ,
,
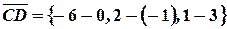 ,
, 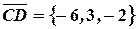 .
.
По правилам действий с векторами, получим:
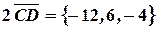 и
и 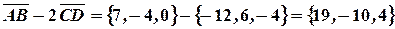 }.
}.
Теперь находим длину искомого вектора:
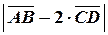 =
= 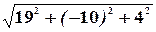 =
= 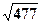 .
.
Пример 2. Даны точки 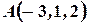 ,
, 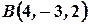 .
.
Найти направляющие косинусы вектора 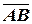 .
.
Решение. Так как 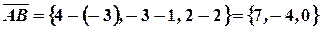 , то
, то 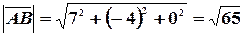 и направляющие косинусы находятся согласно формулам:
и направляющие косинусы находятся согласно формулам:
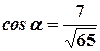 ,
, 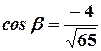 ,
, 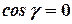 .
.
 2015-06-28
2015-06-28 545
545








