Теорема о независимости к. п. д. обратимых машин от свойств рабочего вещества позволяет установить температурную шкалу, не зависящую от выбора термометрического тела

В соответствии с указанной теоремой величина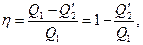

а, следовательно, и отношение Q′₂/Q₁ для цикла Карно, зависят только от температур нагревателя и холодильника.

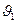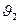Обозначив величины этих температур по некоторой, пока не известной нам шкале через и , можно написать, что

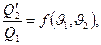(1)

где ƒ(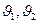) — универсальная (т.е. одинаковая для всех циклов Карно) функция температур нагревателя и холодильника.

Соотно­шение (1) дает возможность определять температуру тел через количества тепла, получаемые и отдаваемые при циклах Карно.

Докажем, что функция (1) обладает следующим свойством:

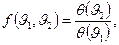(2)

где 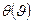есть опять-таки универсальная функция температуры.

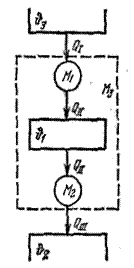
Рассмотрим две обратимые машины M ₁ и M ₂ (рис. 3), холодиль­ник одной из которых служит одновременно нагревателем для другой.

Предположим, что вторая машина отбирает от резервуара с температурой 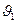такое же количество тепла, какое отдает ему первая машина.

· Для машины M₁ Q ₁ = Q _Ι, Q ′₂ = Q _ΙΙ.

Следовательно, соотношение (1) для этой машины имеет вид

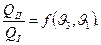(3)

· Для машины M ₂, Q ₁ = Q _ΙI, Q ′₂ = Q _III.

Поэтому согласно (1)

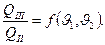(4)

Рассматривая машины M ₁ и М ₂, а также резервуар с температурой 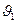как единую обратимую машину, получающую тепло Q ₁, от нагревателя с температурой 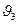и отдающую тепло Q _III холодильнику с температурой 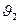, можно написать:

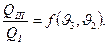(5)

Разделив (5) на (3), получим, что

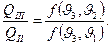
Сравнение этого выражения с (4) приводит к соотношению

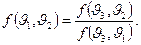(6)

Это соотношение связывает температуры 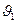и 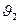двух тел, причем в нем фигурирует температура 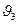третьего тела.

Условившись раз и навсегда о выборе этого тела, т. е. сделав 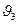неизменной, мы сведем функцию ƒ(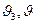), стоящую в числителе и знаменателе формулы (6), к функции одной переменной 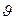. Обозначив эту функцию через 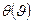, мы придем к формуле (1).

Функция 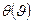зависит только от температуры. Поэтому ее значения можно использовать для характеристики температуры соответствующего тела, т. е. полагать температуру тела равной 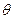, где .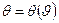

Тогда выражение (1) примет следующий вид:

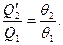(7)

Соотношение (7) положено в основу так называемой термодинамической шкалы температур.

Преимущество этой шкалы заключается в том, что она не зависит от выбора тела (рабочего вещества в цикле Карно), используемого для измерения температуры.

В соответствии с (7) для сопоставления температур двух тел нужно осуществить цикл Карно, используя эти тела в качестве нагревателя и холодильника.

Отношение количества тепла, отданного телу — «холодильнику», к количеству тепла, отобранного от тела — «нагревателя», даст отношение температур рассматриваемых тел.

Для однозначного определения численного значения 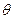необходимо условиться о выборе единицы температуры, т. е. градуса. За абсолютный градус принимается одна сотая разности температур кипящей при атмосфер­ном давлении воды и тающего льда.

Таким образом, градус абсолютной термодинамической шкалы равен градусу идеальной газовой шкалы.

Легко установить, что термодинамическая шкала температур совпадает с идеальной газовой шкалой. Действительно,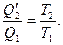

Следовательно, 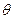пропорциональна Т и, поскольку градус обеих шкал одинаков, 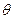= T.