Еквівалентні автомати мережі

Для мережі з n компонентних автоматів можна побудувати еквівалентний автомат А мережі

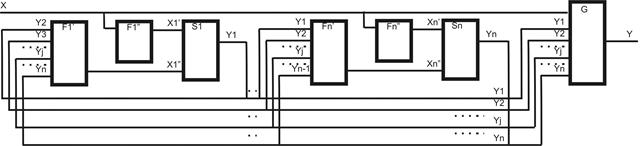
Рис. 21.2. Мережа з n компонентних автоматів

A_N = (S_N, X_N, Y_N, d_N, l_N, {s_0N}),

де X_N = X, S_N = (´_i=1ⁿS_i), іÎ{1, n}, Y_N = Y.

Функція d_N визначається в такий спосіб

d_N: S_N´X_N®S_N чи d(S_N´X_N) = {s_nj = d(s'_nj, x)Îd(S_N´X_N)| s_nj = <s_1j, s_nj, … s_ij, … s_nj> & s’_ij = <s’_1j, s’_2j, … s’_ij, … s’_nj> & s_ij, s’_ijÎS_i для всіх іÎ{1, n}, & s_ij = d_і(s'_іj, <f_i(y_1k, y_2k, …y_ik, …y_nk),
j(X_N)) & y_ik @ s’_ij, для всіх іÎ{1, n}}.

Функція l_N для автомата Мілі визначається в такий спосіб

l_N: S_N´X_N®Y_N чи l_N(S_N´X_N) = {y = l_N(s'_nj, X_NÎd_N(S_N´X_N)| yÎY_N & X_NÎ X_N & s'_nj = <s'_1j, s'_2j, …s’_ij, …s’_nj> & s’_ijÎS_i для всіх іÎ{1, n} & y = g(<у'_1k, у'_2k, …y’_ik, …y’_nk>, X_N) & y’_ik @ s’_ij для всіх іÎ{1, n}}.

Функція l_N для автомата Мура визначається в такий спосіб

l_N: S_N´X_N®Y_N чи l_N(S_N) = {y = l_N(s'_njÎl_N(S_N)| yÎY_N & s'_nj =<s'_1j, s'_2j, …s’_ij, …s’_nj> & s’_ijÎS_i для всіх іÎ{1, n} & y = g<s'_1j, s'_2j, …s’_ij, …s’_nj> = g_N(<y’_1k, y’_2k, …y’_{ik, …} y’_nk > & y’_ik @ s’_ij для всіх
іÎ{1, n}}.

Приклад. Мережа з трьома компонентними автоматами.

f₁ = Æ (не визначена)

f₂:Y₁´Y₃®X’₂ чи X’₂ = f₂(Y₁´Y₃)

f₃:Y₂®X’₃ чи X’₃ = f₃(Y₂)

g:Y₂´Y₃®Y чи Y = g(Y₂´Y₃)

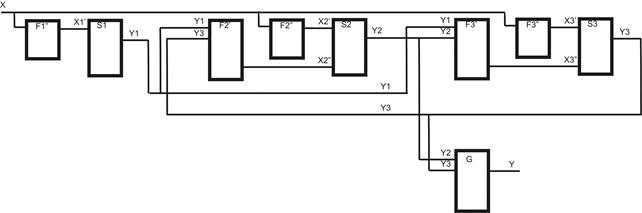
Рис. 21.3. Мережа з трьома компонентними автоматами

Контрольні запитання

1. Що є мережею автоматів, що узагальнює мережа автоматів?

2. Що є компонентним автоматом?

3. Яка різниця між компонентним автоматом та звичайним напівавтоматом?

4. Що є еквівалентним автоматом для мережі автоматів?

5. Як визначити функції переходів та вихідів для еквівалентного автомата мережі автоматів?