Список літератури. 24.1. Новиков Ф.А. Дискретная математика для программистов

Основна

24.1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.81-88.

24.2. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. - С.10-19.

24.3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.504-522.

Додаткова

24.4. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.47-50.

24.5. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. - С.139-150.

Для практичних занять

24.6. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.27-30.

24.7. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1973. - С.30-38.

Лекція 25. Алгебра Жегалкіна. Типи функцій. Логічні схеми

Вступ

Лекція має за мету навести основні поняття алгебри Жегалкіна, функціональної повноти. Розглянути вісім властивостей операцій базису {Å, Ù}, п’ять типів булевих функцій, функціональна замкненість та повнота, критерій Поста. Звернено увагу до канонічної задачі синтезу логічних схем.

У лекції присутні п’ять підрозділів:

25.1. Алгебра Жегалкіна

25.2. Типи булевих функцій

25.3. Функціональна повнота

25.4. Логічні (перемикальні) схеми

25.5. Канонічна задача синтезу логічних схем

25.1. Алгебра Жегалкіна

Алгебра Жегалкіна задана на всій множини булевих функцій на основі двох операції: нерівнозначності Å і кон'юнкції Ù.

Визначення. Алгебра Жегалкіна – цє система А=(В, {Å, Ù}, 1), де основна множина В – цє множина усіх булевих функцій, сигнатура алгебри – {Å, Ù}, додатково алгебру поповнює константа одиниці.

Тип алгебри Жегалкіна - (2, 2), тобто вона не є булевої алгеброю.

В алгебрі Жегалкіна виконуються такі тотожності:

1. хÅу=уÅх; хÙу=уÙх
комутативність.

2. хÅ(уÅz)=(xÅy)Åz; xÙ(yÙz)=(xÙy)Ùz
асоціативність.

3. xÙ(yÅz)=(xÙy)Å(xÙz)
дистрибутивність кон'юнкції.

4. xÅ0=x; xÙ0=0;
xÅ1=`x; xÙ1=x
властивості границь.

5. хÅх=0; хÙх=х
приведення і ідемпотентність.

6. xÅ`x=1; xÙ`x=0
доповнення.

7. xÅ(xÙy)=xÙ`y; xÙ(xÅy)=xÅ(xÙy)
поглинання.

8. xÅ(`yÙz)=хÅу; xÙ(`xÅy)=хÙу
Блейка-Порецького.

9. (xÅy)Ù(xÅ`y)=0; (xÙy)Å(xÙ`y)=x
склеювання.

10. ù(xÅy)=`xÅy=xÅ`y; ù(xÙy)=(xÙy)Å1
де Моргана.

11. xÅy=(xÙ`y)Ú(`xÙy); xÅy=(xÚy)Ù(`xÚ`y)
переклад у булев базис.

12. xÅy=`xÅ`y.

13. xÚy=xÅyÅ(xÙy)
переклад у базис Жегалкіна;

14. xÅy=0Ûx=y.

15. xÅy=zÞxÅz=y або zÅy=x.

Тотожності 4, 6, 13 дозволяють перейти від будь-якої формули булевої алгебри до відповідної їй формули алгебри Жегалкіна, а за допомогою тотожностей 4, 6, 11 можна здійснити зворотний перехід від алгебри Жегалкіна до булевої алгебри.

Приклад. xÙ(`xÚy) = xÙ((1Åx)Úy) = xÙ((1Åx)ÅyÅ(1Åx)Ùy))= xÙ(1Å ÅxÅyÅyÅ(xÙy)) = xÅ(xÙx)Å(xÙyÙx) = xÅxÅ(xÙy) = xy;

1ÅxÅy=`xÅy=(xy)Ú(`x`y).

Система операцій алгебри Жегалкіна {Å, Ù} разом з константою «1» утворює так звану послаблено функціонально повну систему.

25.2. Типи булевих функцій

Визначення. У булевої алгебрі з множини булевих функцій від ²n² змінних f(x₁, x₂,..., x_n) потужності 2^{2^n} виділяються п'ять типів булевих функцій (п’ять класів попередньо повних функцій):

1. Функції, що зберігають константу «0», тобто функції, що на нульових наборах аргументів приймають нульові значення:

f(x₁, x₂,..., x_n)Þf(0, 0,..., 0)=0.

Приклад. f(x₁, x₂)=x₁Ùx₂Þf(0, 0)=0.

2. Функції, що зберігають константу «1», тобто функції, що на одиничних наборах аргументів приймають одиничні значення:

f(x₁, x₂,..., x_n)Þf(1, 1,..., 1)=1.

Приклад. f(x₁, x₂)=x₁Ùx₂Þ f(1, 1)=1.

3. Самоподвійні функції, що приймають протилежні значення на будь-яких двох протилежних наборах:

Приклад. f(x)= ` xÞf(0)=1, f(1)=0.

4. Лінійні функції, що являються в алгебрі Жегалкіна канонічним багаточленом, що не утримує добутків змінних:

f(x₁, x₂,..., x_n)=a₀Å a₁×x₁Åa₂×x₂Å...Åa_n×x_n,

де а₀, а₁, а₂,..., а_n – константи, що приймають значення 0 чи 1

Приклад. f(x)=1Å x₁Å x₂.

5. Монотонні функції, що для будь-яких двох упорядкованих наборів аргументів <x₁₁, x₁₂,..., x_1n> і <x₂₁, x₂₂,..., x_2n>, де <x₁₁, x₁₂,..., x_1n> £ £<x₂₁, x₂₂,.., x_2n>, приймають також упорядковані значення, тобто f(x₁₁, x₁₂,..., x_1n)£ f(x₂₁, x₂₂,..., x_2n).

Приклад. f₁(x₁, x₂)=x₁Úx₂, f₂(x₁, x₂)=x₁Ùx₂, f₃(x₁, x₂)=x₂

<x₁, x₂> f₁: f₂: f₃:

<0, 0> 0 0 0

<0, 1> 1 0 1

<1, 0> 1 0 0

<1, 1> 1 1 1

Крім ціх п’яти типів, викреслюють тип сіметричних функцій.

Визначення. Булева функція симетрична по змінним x_i, x_j, якщо
f(…, x_i,…,x_j,…) = f(…, x_j,…,x_i,…). Булева функція симетрична, якщо вона симетрична по усім парам змінних.

Приклад. Функція f = x₁`x<sub>2</sub>`x₃ Ú `x<sub>1</sub>`x₂x₃ симетрична по змінних x₁ і x₃. Функція f = x₁x₂ Ú x₁x₃ Ú x₂x₃ симетрична.

25.3. Функціональна повнота

Визначення. Система булевих функцій називається функціонально повною, якщо суперпозиція цих функцій дозволяє одержати будь-яку функцію з множини булевих функцій.

Приклад. Система функцій {Ú, Ù, ù } є функціонально повною, але система функцій {Å, Ù} не функціонально повна.

Якщо у функціонально повній системі є функції константи «0» чи константи «1», то вона послаблено функціонально повна. Функціонально повна система функцій утворює базис у логічному просторі.

Приклад. Система функцій {Å, Ù}, що поповнена константою одиниці, тобто {{Å, Ù} 1}, послаблено функціонально повна.

Визначення. Система булевих функцій називається мінімально повним базисом, якщо видалення з неї будь-якої функції перетворює цю систему в неповну.

Приклад. Мінімально повний базис є {Ù, ù }, але система {Ú, Ù, ù } не є мінімально повним базисом.

Визначення. Усяка сукупність функцій алгебри логіки, замкнута щодо суперпозиції, тобто така, що будь-яка суперпозиція функцій із сукупності знову породжує функцію, що належить ції же сукупності, називається функціонально замкнутим класом.

Функціонально замкнуті класи, відмінні від порожнього класу і сукупності всіх можливих булевих функцій, називаються власними функціонально замкнутими класами. Власний функціонально замкнутий клас називається передповним, якщо він не міститься ні в якому функціонально замкнутому класі, що є відмінним від даного класу і класу всіх можливих булевих функцій.

Приклад. Система функцій, що зберегають одиницю, є функціонально замкнутим класом, система функцій, що монотонно убивають, не є функціонально замкнутим класом. Перша система є поперед повною.

Теорема про функціональну повноту (критерій Поста): Для того, щоб система булевих функцій була повною, необхідно і досить, щоб вона включала хоча б одну функцію, що не зберігає константу «0», хоча б одну функцію, що не зберігає константу «1», хоча б одну функцію, що несамоподвійна, хоча б одну функцію, що нелінійна, і хоча б одну функцію, що немонотонна.

Та сама функція може представляти у функціонально повній системі одне чи кілька необхідних властивостей, якщо вона має ці властивості.

Приклад. Властивості елементарних булевих функцій.

Таблиця 25.1.

Булева функція	Фор-мула	Незбер. ”0”	Незбер. ”1”	Несамо-двоїста	Нелі-нійна	Немо-нотонна
Константа “0”	0		+	+
Константа “1”	1	+		+
Заперечення	ù x	+	+			+
Кон'юнкція	x1Ùx2			+	+
Диз'юнкція	x1Úx2			+	+
Сума за модулем “2”	x1Åx2		+	+		+
Штрих Шеффера	x1/x2	+	+	+	+	+
Стрілка Пірса	x1¯x2	+	+	+	+	+

З таблиці видно, що системи функцій {кон ' юнкція, заперечення}, {диз'юнкція, заперечення}, {штрих Шеффера}, {стрілка Пірса} задовольняють теоремі Поста. Система функцій {Ú, Ù, ù} утворює так званий булевий базис.

25.4. Логічні (перемикальні) схеми

Для реалізації булевих функцій розробляються і використовуються релейні і логічні елементи, що є звичайно напівпровідниковими приладами, що виконані за субмікронною технологією. Їхні входи відповідають булевим змінним, виходи - реалізованої функції. Для позначення логічних елементів використовують прямокутники, трикутники, або інші фігури. У полі фігури елемента може бути указана та операція, що він реалізує. Подібно суперпозиції булевих функцій логічні схеми будують з'єднанням логічних елементів.

Приклад. Релейні (контактні) схеми).

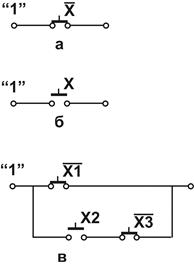
Рис. 25.1. Релейні перемикальні схеми для трьох функцій
а - y₁ =`x; б - y<sub>2</sub> = x; с - у<sub>3</sub> =`x₁Ú(x₂×`x₃)

Приклад. Логічна схема з п’яти елементів.

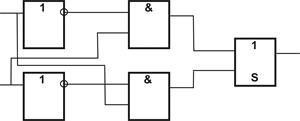
Рис. 25.2. Логічна схема для функції y = (x₁×`x<sub>2</sub>) Ú(`x₁× x₂)

25.5. Канонічна задача синтезу логічних схем

Пристрої, що реалізують елементарні булеві функції, називаються логічними елементами. Логічною схемою називається з'єднання (суперпозиція) логічних елементів.

Задача побудови логічної схеми, що відповідає заданій булевій функції, називається задачею синтезу.

Задача визначення булевої функції для заданої логічної схеми називається задачею аналізу.

Між формулою, що відповідає булевій функції, і логічною схемою, що реалізує формулу, існує взаємно однозначна відповідність. Однак та сама булева функція може бути представлена за допомогою декількох формул, отже, можна побудувати кілька схем, що реалізують ту саму булеву функцію. Такі логічні схеми називаються еквівалентними. Очевидно, що більш простій формулі відповідає і більш проста логічна схема. Прийнято вважати більш простою ту формулу, що містить менше число змінних і логічних операцій. Таким чином, для одержання більш простої логічної схеми необхідно провести спрощення формули логічної функції за допомогою логічних перетворень.

Визначення. Канонічна задача синтезу логічних схем у булевому базисі (Ú, Ù, ù) зводиться до такого:

1. Вихідна булева функція представляється в СДНФ (СКНФ).

2. За допомогою операцій доповнення, поглинання булева функція приводиться до вигляду ДНФ (КНФ), що містить кількість (букв) змінних і знаків операцій, яка не піддається скороченню, тобто тупикової ДНФ (тупикової КНФ) чи ТДНФ (ТКНФ).

3. Для отриманої ТДНФ (ТКНФ) будується логічна схема.

Операції доповнення:

(x₁×x₂)Ú(x₁× ` x<sub>2</sub>)=x<sub>1</sub>; (x<sub>1</sub>Úx<sub>2</sub>) (x<sub>1</sub>Ú ` x₂)=x₁.

Операції поглинання:

x₁Ú(x₁×x₂)=x₁; x₁(x₁Úx₂)=x₁.

У результаті застосування операцій доповнення і поглинання виходять формули, для яких подальші операції доповнення і поглинання застосувати неможна, тобто тупикові форми - ТДНФ і ТКНФ. Серед тупикових форм знаходиться і мінімальна (МДНФ і МКНФ), причому мінімальних форм може бути кілька. Ще один крок у мінімізації – одержання форми у дужках (СкНФ).

Приклад.y=x₁x₂ ` x<sub>3</sub>Ú ` x₁x₂x₃Úx₁x₂x₃ СДНФ

y=x₁x₂ ` x<sub>3</sub>Ú ` x₁x₂x₃Úx₁x₂x₃Úx₁x₂x₃

y=x₁x₂Úx₂x₃ МДНФ

y=x₂(x₁Úx) СкНФіф (і МКНФ).

Контрольні запитання

1. Що називається алгеброю Жегалкіна, що є основною множиною та сигнатурою алгебри Жегалкіна?

2. Які вісім основних тотожностей алгебри Жегалкіна існують?

3. Як привести формулу функції з булевої алгебри в алгебру Жегалкіна та навпаки?

4. Які типи булевих функцій існують?

5. Як визначити належність функції до кожного з п’яти типів?

6. Яка система булевих функцій є функціонально повною, послаблено функціонально повною?

7. Що є базисом у логічному просторі, мінімально повним базисом?

8. Яка система функцій є функціонально замкнутою?

9. Які класи називають власними функціонально замкнутими класами, попередповними класами?

10. Що наголошує критерій Поста?

11. Що є логічною схемою?

12. Як відрізняються задачі аналізу та синтезу? Що є канонічною задачею синтезу логічних схем?