2015-06-28
570
Эта задача имеет большое значение в практических применениях. К ней сводятся многие задачи выбора наиболее экономичного (с точки зрения расстояния или стоимости) маршрута на имеющейся карте дорог, наиболее экономичного способа перевода динамической системы из одного состояния в другое и т.д. Существует много математических способов решения, но часто методы, основанные на теории графов, наименее трудоемки.
Рассмотрим задачу о кратчайшем пути. Пусть дан G(X), дугам которого приписаны веса (расстояния, стоимости), задаваемые матрицей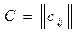 
. Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной вершины s Î X до заданной конечной вершины t Î X при условии, что такой путь существует. В общем случае возможно Сij > 0, Сij <0, Сij = 0. Единственное ограничение состоит в том, чтобы в графе G(X) не было циклов с отрицательным суммарным весом.
Приведем очень простой и эффективный алгоритм Дейкстры решения этой задачи для случая Сij ³ 0 " i, j. Алгоритм основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от s к этой вершине. Величины этих пометок постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации точно одна из временных пометок становится постоянной. Это означает, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.
|
|
|
Опишем этот алгоритм.
Пусть l(xi) – пометка вершины xi. Алгоритм Дейкстры состоит из следующих этапов.
