Функция f (x1, x2,..., xn), принимающая два значения: 0 и 1 и зависящая от переменных, каждая из которых может принимать значения 0 и 1, называется булевой или переключательной. Из определения следует, что область определения булевой функции – совокупность всевозможных n-мерных наборов из нулей и единиц, а для её задания достаточно указать, какие значения функции соответствуют каждому из наборов (табл. 3.3).
Таблица 3.3 – Задание булевой функции
| x1 | x2 | ... | xn-1 | xn | f (x1, x2,...,xn-1, xn) |
| ... | f (0, 0,...,0, 0) | ||||
| ... | f (0, 0,...,0, 1) | ||||
| ... | ... | ... | ... | ... | .................……… |
| ... | f (1, 1,...,1, 0) | ||||
| ... | f (1, 1,...1, 1) |
Порядок расположения наборов, принятый в таблице, называется стандартным или естественным. При таком порядке каждому набору
[Ò1] a = (a1,...,an), где ai есть 0 или 1, ставится в соответствие число
N = a1 2n-1 +... + an-1 2 + an .
Наборам (0, 0,...,0, 0), (0, 0,...,0, 1),..., (1, 1,...,1, 1) соответствуют числа 0, 1,..., 2n-1. Естественным порядком будет расположение наборов в порядке возрастания соответствующих им чисел. Десятичное число, соответствующее входному набору, является его номером. Поэтому очевидно, что количество k входных наборов для булевой функции n переменных равно k=2n. Количество же различных функций n переменных можно определить из следующих соображений. Каждая функция задается набором своих k значений (для k входных наборов), которому также можно поставить в соответствие k-разрядное двоичное число. Располагая теперь в таблице функции в порядке возрастания соответствующих им чисел, мы получим все возможные различные функции. Количество таких функций будет равно 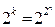 .
.
Рассмотрим другие способы задания булевых функций. Сначала познакомимся с функциями одной и двух переменных, которые часто употребляются в математической логике и кибернетике, их можно считать «элементарными» функциями (табл. 3.4, 3.5).
Таблица 3.4 – Булевы функции одной переменной
| x | g1(x) | g2(x) | g3(x) | g4(x) | g1(x), g4(x) – константы 0 и 1, |
| g2(x) = x, | |||||
| g3(x) = `x (отрицание x). |
Таблица 3.5 – Булевы функции двух переменных
| x1 | x2 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
Следует отметить, что к функциям двух переменных относятся и такие, которые в действительности зависят от одной переменной или не зависят ни от одной.
Функции f1, f16 – константы 0 и 1. Они не зависят существенно ни от одной переменной.
Функции f4 = х1, f11 =`х2, f6 = х2, f13 =`х1 зависят существенно только от одной переменной.
f2 = х1 ٨ х2 – конъюнкция или логическое умножение (знак «٨» можно заменять на «∙», либо опускать).
f8 = х1 ٧ х2 – дизъюнкция или логическое сложение.
f10 – эквивалентность, х1 ~ х2.
f7 = х1 Å х2 или х1 + х2 (mod 2) – сложение по модулю два.
f12, f14 – импликация, х2 ® х1 и х1 ® х2.
f15 – штрих Шеффера, х1 | х2.
f9 – стрелка Пирса, х1 ¯ х2 (другое название – функция Вебба).
 f3, f5 – функции запрета х1 и х2 соответственно. f3 = х1 ® х2,
f3, f5 – функции запрета х1 и х2 соответственно. f3 = х1 ® х2,
 f5 = х2 ® х1.
f5 = х2 ® х1.
Исходя из элементарных функций можно строить формулы, т.е. рассматривать функции от функций например, (x1 Å x2)`х2) ® х3.
 2015-06-28
2015-06-28 519
519







