Заданы векторы 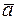 ,
, 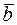 ,
, 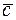 и
и 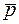 своими координатами в некотором базисе (таблица 3). Показать, что векторы
своими координатами в некотором базисе (таблица 3). Показать, что векторы 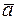 ,
, 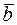 ,
, 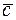 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 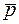 в базисе
в базисе 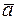 ,
, 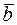 ,
, 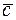 .
.
Таблица № 3
| № варианта |
|
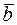
|
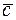
|
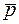
|
| (0,1,2) | (1,0,1) | (-1,2,4) | (-2,4,7) | |
| (1,3,0) | (2,-1,1) | (0,-1,2) | (6,12,-1) | |
| (2,1,-1) | (0,3,2) | (1,-1,1) | (1,-4,4) | |
| (4,1,1) | (2,0,-3) | (-1,2,1) | (-9,5,5) | |
| (-2,0,1) | (1,3,-1) | (0,4,1) | (-5,-5,5) | |
| (5,1,0) | (2,-1,3) | (1,0,-1) | (13,2,7) | |
| (0,1,1) | (-2,0,1) | (3,1,0) | (-19,-1,7) | |
| (1,0,2) | (0,1,1) | (2,-1,4) | (3,-3,4) | |
| (3,1,0) | (-1,2,1) | (-1,0,2) | (3,3,-1) | |
| (-1,2,1) | (2,0,3) | (1,1,-1) | (-1,7,-4) | |
| (1,1,4) | (0,-3,2) | (2,1,-1) | (6,5,-14) | |
| (1,-2,0) | (-1,1,3) | (1,0,4) | (6,-1,7) | |
| (1,0,5) | (-1,3,2) | (0,-1,1) | (5,15,0) | |
| (1,1,0) | (0,1,-2) | (1,0,3) | (2,-1,11) | |
| (1,0,2) | (-1,0,1) | (2,5,-3) | (11,5,-3) | |
| (2,0,1) | (1,1,0) | (4,1,2) | (8,0,5) | |
| (0,1,3) | (1,2,-1) | (2,0,-1) | (3,1,8) | |
| (1,2,-1) | (3,0,2) | (-1,1,1) | (8,1,12) | |
| (1,4,1) | (-3,2,0) | (1,-1,2) | (-9,-8,-3) | |
| (0,1,-2) | (3,-1,1) | (4,1,0) | (-5,9,-13) | |
| (0,5,1) | (3,2,-1) | (-1,1,0) | (-15,5,6) | |
| (1,0,1) | (0,-2,1) | (1,3,0) | (8,9,4) | |
| (2,1,0) | (1,-1,0) | (-3,2,5) | (23,-14,-30) | |
| (2,1,0) | (1,0,1) | (4,2,1) | (3,1,3) | |
| (0,3,1) | (1,-1,2) | (2,-1,0) | (-1,7,0) | |
| (1,-1,2) | (3,2,0) | (-1,1,1) | (11,-1,4) | |
| (1,1,4) | (-3,0,2) | (1,2,-1) | (-13,2,18) | |
| (0,-2,1) | (3,1,-1) | (4,0,1) | (0,-8,9) | |
| (0,1,5) | (3,-1,2) | (-1,0,1) | (8,-7,-13) | |
| (1,0,1) | (1,-2,0) | (0,3,1) | (2,7,5) |
 Образец решения задачи № 3
Образец решения задачи № 3
Пусть векторы имеют следующие координаты 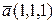 ,
, 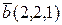 ,
, 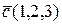 ,
, 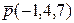 .
.
Покажем, что векторы 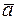 ,
, 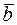 ,
, 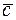 образуют базис. Как известно, в пространстве любые три некомпланарных вектора образуют базис. Для того чтобы векторы
образуют базис. Как известно, в пространстве любые три некомпланарных вектора образуют базис. Для того чтобы векторы 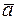 ,
, 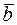 ,
,  были некомпланарными достаточно, чтобы их смешанное произведение не равнялось нулю.
были некомпланарными достаточно, чтобы их смешанное произведение не равнялось нулю.
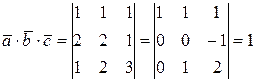 .
.
Найдём координаты вектора 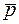 в базисе
в базисе  ,
, 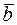 ,
, 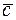 . Представим вектор
. Представим вектор 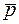 в виде:
в виде:
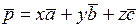 .
.
Получаем систему линейных уравнений:
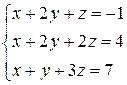 .
.
Решим эту систему по правилу Крамера, получаем:
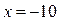 ,
, 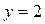 ,
, 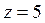 .
.
 2015-06-28
2015-06-28 476
476








