Решение. Векторы будут некомпланарными, если

В екторы 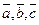будут некомпланарными, если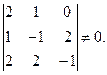

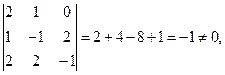т.е. тройку векторов 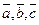можно взять в качестве базиса.

Разложим вектор 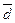по базису :

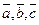где 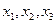─ неизвестные координаты вектора 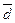в базисе .

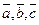Подставим в это равенство координаты векторов:

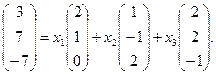
Из равенства векторов следует:

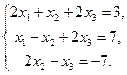
Решая эту систему любым методом, найдем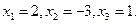

Следовательно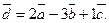

Заметим, что полученное разложение вектора 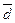по базису 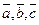единственное, т.к. система имеет единственное решение (главный определитель системы не равен нулю).