Решение.
1) 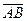 =
= 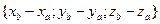 =
= 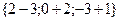
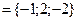 ,
,
тогда 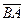
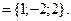 .
.
2) 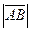 =
= 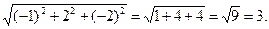
Очевидно 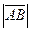 =
= 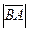 = 3.
= 3.
3) Орт 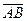 обозначим
обозначим 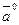 . Для получения вектора единичной длины надо каждую координату вектора поделить на его длину.
. Для получения вектора единичной длины надо каждую координату вектора поделить на его длину.
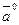
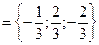 .
.
5) Т.к. 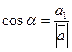 ,
, 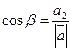 ,
, 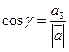 , то
, то 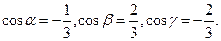
Действия с векторами.
Линейными операциями над векторами являются сложение векторов и умножение вектора на число.
· Векторы 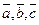 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  (хотя бы одно из которых не равно нулю), что выполняется равенство
(хотя бы одно из которых не равно нулю), что выполняется равенство
· 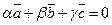 .
.
· Векторы 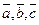 называются линейно независимыми, если данное равенство выполняется только если
называются линейно независимыми, если данное равенство выполняется только если 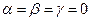 .
.
· Для линейной зависимости двух векторов необходима и достаточна их коллинеарность. Для линейной зависимости трех векторов ─ компланарность.
· Совокупность трех (двух) линейно независимых векторов 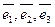 трехмерного пространства (плоскости), взятых в определенном порядке, образует базис.
трехмерного пространства (плоскости), взятых в определенном порядке, образует базис.
· Любой вектор единственным образом представляется в виде суммы
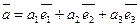 . Числа
. Числа 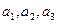 ─ координаты вектора
─ координаты вектора 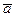 в данном базисе.
в данном базисе.
В прямоугольной системе координат базисом является тройка векторов 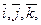
где 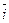 ─ орт оси
─ орт оси 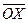 ;
; 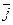 ─ орт оси
─ орт оси 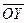 ; ─
; ─ 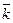 орт оси
орт оси 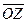 .
.
Два вектора равны, когда равны соответствующие координаты в одном и том же базисе.
Координаты суммы векторов равны суммам соответствующих координат.
Координаты произведения вектора на число равны произведениям координат данного вектора на это число.
· Необходимым и достаточным условием коллинеарности векторов является пропорциональность их соответствующих координат.
· Необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, строками (столбцами) которого являются координаты данных векторов.
Пример 2. Даны векторы 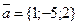 и
и 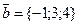 .
.
Найти проекции на координатные оси векторов:
1) 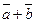 ; 2)
; 2) 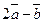 ; 3)
; 3) 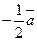 .
.
 2015-06-28
2015-06-28 324
324







