Бином Ньютона. Для доказательства формулы можно рассмотреть выражение (a + b) ∙ (a + b) ∙ ∙ (a + b)

(a + b)ⁿ =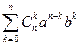

Для доказательства формулы можно рассмотреть выражение (a + b) ∙ (a + b) ∙… ∙ (a + b). Подсчитаем, сколько раз в этом выражении встретится b^k.

Это выражение встретится столько раз, сколько способов выбрать k скобок, из которых возьмём b, среди всех n скобок. А это количество способов равно .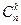

Из оставшихся (n-k) скобок выберем (n-k) множителей a. Таким образом, получим слагаемое 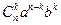. Так сделаем для k от 0 до n.

Свойства биномиальных коэффициентов

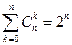
Доказательство.

Подставим в бином Ньютона a = b = 1.

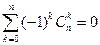
Доказательство.

Подставим в бином Ньютона a = 1, b = -1.