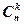 - число k-элементных подмножеств n-элементного множества (читается как «число сочетаний из n по k»).
- число k-элементных подмножеств n-элементного множества (читается как «число сочетаний из n по k»).
Для нахождения количества сочетаний без повторений воспользуемся формулой для размещений без повторений.
Упорядоченных наборов k элементов из n существует n!/(n-k)! Если будем рассматривать неупорядоченные наборы, то каждый из них сосчитаем по k! раз.
Поэтому неупорядоченных наборов в k! раз меньше, чем упорядоченных.
Поэтому количество неупорядоченных наборов вычисляется по формуле: n!/((n-k)!k!).
Пример.
Сколько способов выбрать трёх дежурных из 25 человек?
Можно вычислять по формуле: 25!/(22!∙3!)
Можно и с помощью логических рассуждений. Первого дежурного можно выбрать 25 способами, второго – 24 способами, третьего – 22 способами. Всего получаем 25 ∙ 24 ∙ 22 способа.
Переход к дополнению
В некоторых случаях проще вычислить количество элементов, которые нам не подходят, а затем вычесть их количество из общего числа элементов.
Пример.
Сколько существует 5-значных чисел, в которых есть хотя бы одна чётная цифра?
 2015-06-28
2015-06-28 814
814








