В некоторых случаях бывает удобно выразить булеву функцию только через конъюнкцию, дизъюнкцию и отрицание.
Например, это удобно из-за того, что выражения с этими операциями удобно подставлять одно в другое.
Для вычисления СКНФ и СДНФ нам пригодится только что построенная таблица.
| x | y | z | 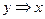 | 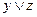 | f | СДНФ | СКНФ |
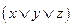 | |||||||
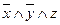 | |||||||
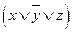 | |||||||
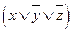 | |||||||
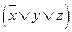 | |||||||
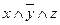 | |||||||
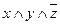 | |||||||
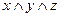 |
Правило построения СДНФ: выбрать те и только те строки, в которых значение функции равно 1, затем в этих строках записать конъюнкцию x, y, z по следующему правилу:
Если соответствующая переменная равна 0, то пишем её с отрицанием, если она равна 1, то пишем без отрицания.
Например, во второй строке мы пишем 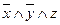 , поскольку в соответствующей строке были значения x = 0, y = 0, z = 1.
, поскольку в соответствующей строке были значения x = 0, y = 0, z = 1.
СДНФ записывают как дизъюнкцию этих выражений. При этом иногда операцию конъюнкции не пишут, подобно тому как для умножения не пишут операцию умножения.
В итоге получаем: СДНФ = 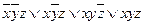 .
.
Построение СКНФ в некотором смысле двойственно к построению СКНФ.
Вместо строк со значением 1 берём строки со значением 0, вместо дизъюнкции – конъюнкция, а вместо конъюнкции дизъюнкцию.
И одно принципиальное отличие – там, где значение переменной равно 0, мы берём её без отрицания, а там, где это значение равно 1, берём с отрицанием. Сравните первую и третью строки, выражения в которых равны соответственно 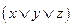 и
и 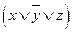 .
.
Выражение для СКНФ можно получить, перемножив все эти дизъюнкции.
СКНФ = 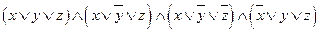 .
.
Следующее важное действие – упростить СДНФ.
Это можно сделать с помощью действий, аналогичных вынесению множителя за скобку.
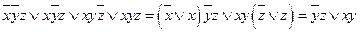
Итак, упрощённая форма СДНФ в данном случае равна 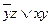 .
.
Показать логическую схему, причём написать, что для первоначальной записи потребовалось бы очень много элементов: импликация, эквивалентность, и так далее. А для СКНФ достаточно трёх элементов: И, ИЛИ и НЕ.
Привести пример составления схемы для СДНФ и для упрощённой ДНФ.
Но, как во многих задачах на упрощение, возникает вопрос: можно ли упростить выражение дальше? Точнее сказать – можно ли получить выражение, содержащее ещё меньше букв и равное данному?
Ответ даёт метод минимизирующих карт.
Для его применения составьте таблицу такого вида.
| f | Значения переменных | x | y | z | xy | xz | yz | xyz |
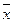 | 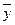 | 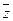 | 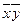 | 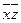 | 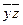 | 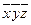 | ||
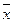 | 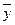 | z | 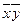 | 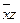 | 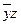 | 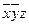 | ||
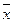 | y | 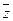 | 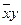 | 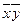 | 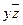 | 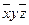 | ||
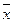 | y | z | 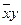 | 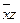 | yz | 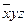 | ||
| x | 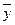 | 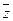 | 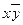 | 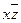 | 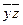 | 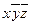 | ||
| x | 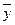 | z | 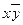 | xz | 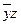 | 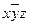 | ||
| x | y | 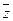 | xy | 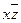 | 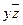 | 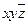 | ||
| x | y | z | xy | xz | yz | xyz |
Каждую переменную, x, y и z, мы снабжаем или не снабжаем отрицанием в соответствии со значениями переменных.
Например, если во втором столбце 001, то x и y с отрицаниями, а z – без отрицания.
А в остальных столбцах переменные сопровождаются отрицаниями в соответствии с третьим, четвёртым и пятым столбцами.
Теперь производим вычёркивание по следующему принципу.
Сначала вычёркиваем все строки, в которых значение функции равно нулю. В данном примере вычёркиваются строки с номерами 1, 3, 4 и 5.
Затем в каждом столбце, если элемент был один раз вычеркнут, он вычёркивается во всех оставшихся клетках столбца. Например, если во второй сверху клетке шестого столбца элемент 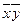 был вычеркнут, то в третьей сверху клетке его также вычеркнем.
был вычеркнут, то в третьей сверху клетке его также вычеркнем.
Теперь из оставшихся элементов, взяв по одному элементу из строки, составим самое короткое выражение.
В данном примере из второй и шестой строк имеет смысл взять два одинаковых выражения 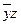 , а из седьмой и восьмой строк – два одинаковых выражения xy, поскольку при вычислении дизъюнкции получим:
, а из седьмой и восьмой строк – два одинаковых выражения xy, поскольку при вычислении дизъюнкции получим: 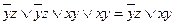 .
.
Рекомендуется сначала найти упрощённое выражение методом минимизирующих карт, а затем производить упрощение СДНФ алгебраическими преобразованиями.
Если преобразования дали такой же ответ, что и метод минимизирующих карт, это добавляет уверенности в ответе.
Если они дали ответ длиннее, то, возможно, вы не до конца использовали возможности упрощения.
А если преобразования дали ответ короче, чем метод минимизирующих карт, то такая ситуация теоретически противоречива: метод минимизирующих карт даёт самую короткую форму записи.
В качестве упражнения на булевы функции можно рассматривать вычисление функции 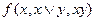 , где f – функция от трёх переменных.
, где f – функция от трёх переменных.
Задачу можно решать двумя способами.
Первый способ: найти значения выражений 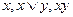 для всех значений пары x, y. Затем подставить полученные значения в функцию от трёх переменных.
для всех значений пары x, y. Затем подставить полученные значения в функцию от трёх переменных.
Например: если x = y = 0, то 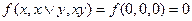 (по таблице истинности для функции f).
(по таблице истинности для функции f).
Дополнительное условие для этой задачи: по таблице истинности необходимо определить формулу для полученной функции от двух переменных. Например, xy или x XOR y.
Второй способ: подставить в исходную формулу для функции (например, 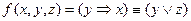 ) вместо переменной y выражение
) вместо переменной y выражение 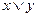 , а вместо переменной z выражение
, а вместо переменной z выражение 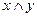 , затем упростить выражение.
, затем упростить выражение.
 2015-06-28
2015-06-28 1785
1785








