1. Булевой функцией от n переменных называется функция, определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение.
а) 0; б) 1; в) 0 или 1; г) любые целые;
2. Булева функция называется монотонной, если из х 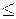 у следует
у следует
а) 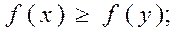 б)
б) 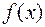 >
> 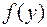 ; в)
; в) 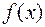
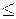
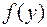 ; г)
; г) 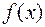 <
< 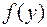 ;
;
3. Выражение 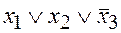 называют
называют
а) элементарной дизъюнкцией; б) элементарной конъюнкцией.
4. Результатом упрощения д.н.ф. 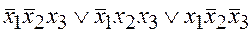 является форма:
является форма:
а) 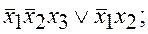 б)
б) 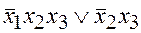 ; в)
; в) 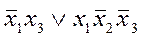 .
.
5. Функцией, двойственной к функции 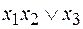 , является
, является
а) 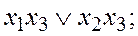 б)
б) 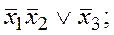 в)
в) 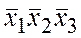
Глава IV. Элементы математической логики
 2015-06-28
2015-06-28 360
360








